Trójkąty napięć, oporów i mocy
Każdy, kto ma pojęcie o diagramach wektorowych, z łatwością zauważy, że można na nich bardzo wyraźnie wyróżnić prostokątny trójkąt napięciowy, którego każda strona odzwierciedla: całkowite napięcie obwodu, napięcie rezystancji czynnej i napięcie na reaktancji.
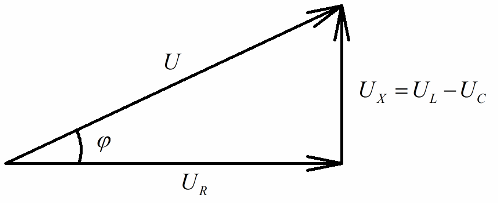
Zgodnie z twierdzeniem Pitagorasa zależność między tymi napięciami (między całkowitym napięciem obwodu a napięciem jego odcinków) będzie wyglądać następująco:
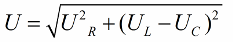
Jeśli następnym krokiem jest podzielenie wartości tych napięć przez prąd (prąd przepływa równo przez wszystkie sekcje obwodu szeregowego), to przez Prawo Ohma otrzymujemy wartości oporów, czyli teraz możemy mówić o trójkącie prostokątnym oporów:
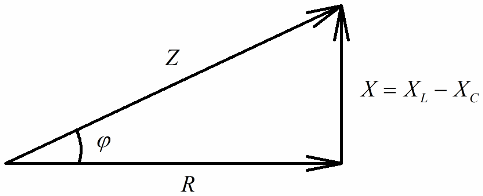
W podobny sposób (jak w przypadku napięć), korzystając z twierdzenia Pitagorasa, można ustalić zależność między impedancją obwodu a reaktancjami. Zależność zostanie wyrażona następującym wzorem:
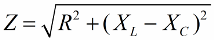
Następnie mnożymy wartości rezystancji przez prąd, w rzeczywistości zwiększymy każdy bok prawego trójkąta określoną liczbę razy. W rezultacie otrzymujemy trójkąt prostokątny o pojemnościach:
Moc czynna uwalniana na rezystancji czynnej obwodu związana z nieodwracalną przemianą energii elektrycznej (w ciepło, przy wykonywaniu pracy w instalacji) będzie jednoznacznie związana z mocą bierną zaangażowaną w odwracalną przemianę energii (tworzenie pól magnetycznych i elektrycznych w cewkach i kondensatorach) oraz przy pełnej mocy dostarczanej do instalacji elektrycznej.
Moc czynna mierzona jest w watach (W), moc bierna — w warysach (VAR — woltamper reaktywny), całkowita — w VA (woltamper).
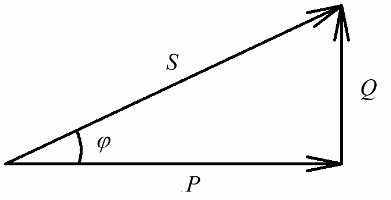
Zgodnie z twierdzeniem Pitagorasa mamy prawo napisać:
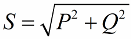
Zwróćmy teraz uwagę na fakt, że w trójkącie mocy występuje kąt phi, którego cosinus można łatwo wyznaczyć przede wszystkim z mocy czynnej i mocy pozornej. Cosinus tego kąta (cos phi) zwany współczynnikiem mocy. Pokazuje, jaka część całkowitej mocy jest brana pod uwagę podczas wykonywania użytecznych prac w instalacji elektrycznej i nie jest zwracana do sieci.
Oczywiście wyższy współczynnik mocy (maksymalny jeden) wskazuje na wyższą sprawność konwersji energii dostarczanej do zakładu do pracy. Jeśli współczynnik mocy wynosi 1, cała dostarczona energia jest wykorzystywana do wykonania pracy.
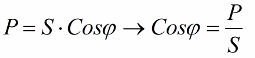
Otrzymane wskaźniki pozwalają na wyrażenie poboru prądu przez instalację poprzez współczynnik mocy, moc czynną oraz napięcie sieciowe:
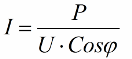
Zatem im mniejszy cosinus phi, tym więcej prądu potrzebuje sieć do wykonania określonej pracy. W praktyce współczynnik ten (maksymalny prąd sieci) ogranicza przepustowość linii transmisyjnej, a zatem im niższy współczynnik mocy, tym większe obciążenie linii i mniejsza użyteczna szerokość pasma (niski cosinus phi prowadzi do ograniczenia). Straty Joule'a w liniach elektroenergetycznych o malejącym cosinusie phi można zobaczyć z następującego wzoru:
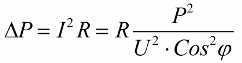
Na czynnej rezystancji R linii transmisyjnej straty rosną tym bardziej, im wyższy jest prąd I, mimo że jest on reaktywny na obciążenie. Dlatego możemy powiedzieć, że przy niskim współczynniku mocy koszt przesyłu energii elektrycznej po prostu wzrasta. Oznacza to, że zwiększanie cosinus phi jest ważnym narodowym zadaniem gospodarczym.
Pożądane jest, aby składowa bierna całkowitej mocy zbliżała się do zera.W tym celu dobrze byłoby zawsze używać silników elektrycznych i transformatorów przy pełnym obciążeniu i wyłączać je pod koniec użytkowania, aby nie pracowały na biegu jałowym. Bez obciążenia silniki i transformatory mają bardzo niski współczynnik mocy. Jednym ze sposobów na zwiększenie cosinus phi u użytkowników jest użycie banki kondensatorów I kompensatory synchroniczne.
