Straty i spadki napięć – czym się różnią

W zwykłym życiu człowieka słowa „utrata” i „upadek” używane są na określenie faktu zmniejszenia się pewnych osiągnięć, ale oznaczają inną wartość.

W tym przypadku „straty” oznaczają utratę części, uszkodzenie, zmniejszenie rozmiaru do wcześniej osiągniętego poziomu. Straty są niepożądane, ale można je tolerować.

Słowo „upadek” rozumiane jest jako poważniejsza krzywda związana z całkowitym pozbawieniem praw. Zatem nawet sporadycznie występujące straty (np. portfela) w czasie mogą doprowadzić do spadku (na przykład poziomu życia materialnego).

W związku z tym rozważymy to pytanie w odniesieniu do napięcia sieci elektrycznej.

Jak powstają straty i spadki napięcia

Energia elektryczna jest przesyłana na duże odległości liniami napowietrznymi z jednej podstacji do drugiej.

Linie napowietrzne są przeznaczone do przesyłania dopuszczalnej mocy i są wykonane z drutów metalowych o określonym materiale i przekroju. Tworzą obciążenie rezystancyjne o wartości rezystancji R i obciążenie reaktywne X.

Stoi po stronie odbiorczej transformatorkonwersja energii elektrycznej.Jego cewki mają aktywną i wyraźną rezystancję indukcyjną XL. Strona wtórna transformatora obniża napięcie i przekazuje je dalej do odbiorników, których obciążenie wyrażone jest wartością Z i ma charakter czynny, pojemnościowy i indukcyjny. Wpływa to również na parametry elektryczne sieci.

Napięcie przyłożone do przewodów wsporczych linii napowietrznej, znajdujących się najbliżej podstacji elektroenergetycznej, pokonuje rezystancję bierną i czynną obwodu w każdej fazie i wytwarza w nim prąd, którego wektor odbiega od wektora przyłożone napięcie o kąt φ.

Charakter rozkładu napięć i przepływu prądów wzdłuż linii dla symetrycznego trybu obciążenia pokazano na zdjęciu.

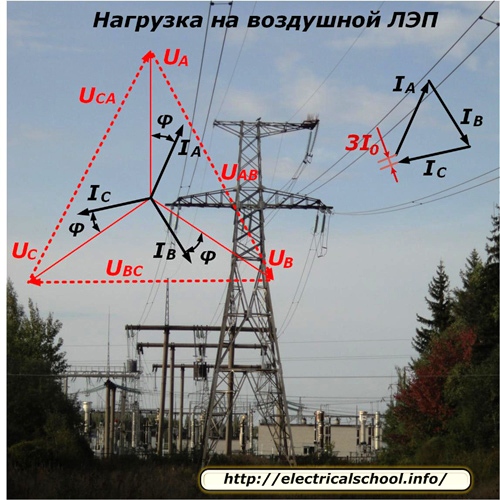
Ponieważ każda faza linii zasila inną liczbę odbiorców, którzy są również losowo odłączani lub podłączani do pracy, technicznie bardzo trudno jest idealnie zrównoważyć obciążenie faz. Zawsze występuje w nim nierównowaga, która jest określana przez dodanie wektorów prądów fazowych i zapisywana jako 3I0. W większości obliczeń jest to po prostu ignorowane.

Energia zużywana przez podstację nadawczą jest częściowo zużywana na pokonanie oporu linii i dociera do strony odbiorczej z niewielkimi zmianami. Frakcja ta charakteryzuje się stratami i spadkami napięcia, których wektor ma niewielką amplitudę i jest przesunięty o kąt w każdej fazie.

Jak obliczane są straty i spadki napięcia

Aby zrozumieć procesy zachodzące podczas przesyłania energii elektrycznej, forma wektorowa jest wygodna do przedstawienia głównych cech. Na tej metodzie opierają się również różne matematyczne metody obliczeniowe.

Aby uprościć obliczenia w układ trójfazowy jest reprezentowany przez trzy równoważne obwody jednofazowe. Metoda ta dobrze sprawdza się przy obciążeniu symetrycznym i pozwala na analizę procesów w przypadku jego awarii.

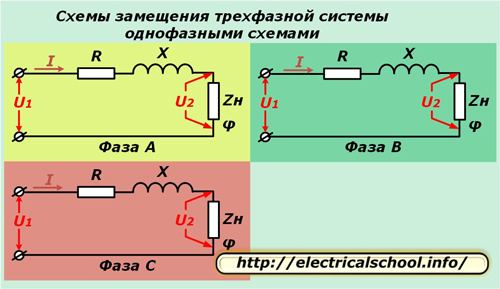
Na powyższych schematach czynna R i reaktancja X każdego przewodu linii są połączone szeregowo ze złożoną rezystancją obciążenia Zn charakteryzującą się kątem φ.

Dodatkowo wykonywane jest obliczenie strat i spadków napięcia w jednej fazie. Aby to zrobić, musisz określić dane. W tym celu wybiera się stację odbierającą energię, której dopuszczalne obciążenie musi być już określone.

Wartość napięcia dowolnego systemu wysokiego napięcia jest już wskazana w książkach referencyjnych, a rezystancje przewodów są określone przez ich długość, przekrój, materiał i konfigurację sieci. Maksymalny prąd w obwodzie jest ustalony i ograniczony właściwościami przewodów.

Zatem, aby rozpocząć obliczenia, mamy: U2, R, X, Z, I, φ.

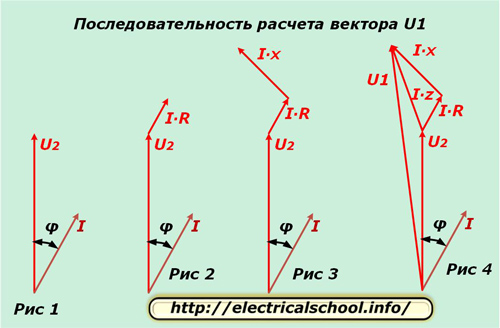
Bierzemy jedną fazę, na przykład „A” i rozdzielamy dla niej na płaszczyźnie zespolonej wektory U2 i I, przesunięte o kąt φ, jak pokazano na rysunku 1. Różnica potencjałów w rezystancji czynnej przewodnika pokrywa się w kierunku z prądem i co do wielkości wyznacza się z wyrażenia I ∙ R. Odkładamy ten wektor od końca U2 (ryc. 2).

Różnica potencjałów w reaktancji przewodnika różni się od kierunku prądu o kąt φ1 i jest obliczana z iloczynu I ∙ X. Odkładamy ją od wektora I ∙ R (ryc. 3).

Przypomnienie: dla dodatniego kierunku obrotu wektorów w płaszczyźnie zespolonej przyjmuje się ruch przeciwny do ruchu wskazówek zegara. Prąd płynący przez obciążenie indukcyjne opóźnia się o kąt z przyłożonym napięciem.

Na rysunku 4 pokazano wykres wektorów różnicy potencjałów na całkowitą rezystancję przewodu I ∙ Z oraz napięcie na wejściu obwodu U1.

Teraz możesz porównać wektory wejściowe z równoważnym obwodem i obciążeniem. Aby to zrobić, umieść powstały diagram poziomo (ryc. 5) i narysuj łuk od początku o promieniu modułu U1, aż przetnie się on z kierunkiem wektora U2 (ryc. 6).

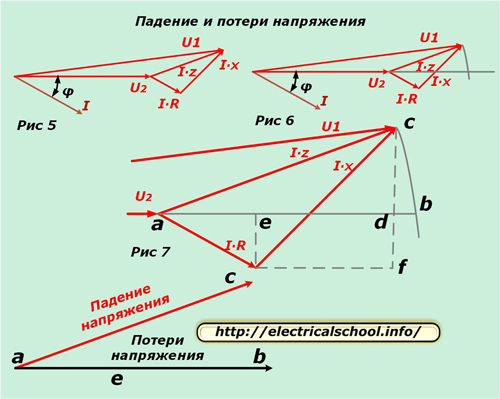
Rycina 7 przedstawia powiększenie trójkąta dla większej czytelności oraz narysowanie linii pomocniczych, wskazujących charakterystyczne punkty przecięcia z literami.

Na dole rysunku pokazano, że wynikowy wektor ac nazywa się spadkiem napięcia, a ab stratą. Różnią się wielkością i kierunkiem. Jeśli wrócimy do pierwotnej skali, zobaczymy, że ac otrzymujemy w wyniku geometrycznego odejmowania wektorów (U2 od U1), a ab jest arytmetyczne. Proces ten pokazano na poniższym rysunku (ryc. 8).

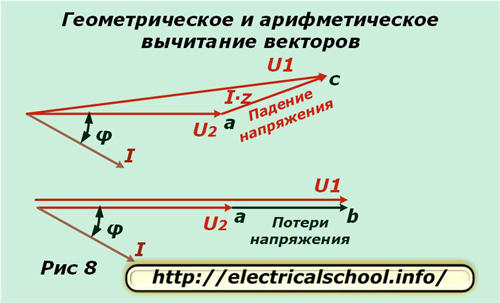
Wyprowadzanie wzorów do obliczania strat napięciowych

Wróćmy teraz do rysunku 7 i zauważmy, że segment bd jest bardzo mały. Z tego powodu jest ona pomijana w obliczeniach i strata napięcia jest obliczana na podstawie długości segmentu ad. Składa się z dwóch odcinków linii ae i ed.

Skoro ae = I ∙ R ∙ cosφ i ed = I ∙ x ∙ sinφ, to spadek napięcia dla jednej fazy można obliczyć ze wzoru:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Jeżeli przyjmiemy, że obciążenie jest symetryczne we wszystkich fazach (pomijając warunkowo 3I0), możemy metodami matematycznymi obliczyć stratę napięcia w linii.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Jeśli prawą stronę tego wzoru pomnożymy i podzielimy przez napięcie sieciowe Un, to otrzymamy wzór, który pozwoli nam wykonać p Obliczenie strat napięcia przez zasilacz.

∆Ul = (P ∙ r + Q ∙ x) / Un

Wartości mocy czynnej P i mocy biernej Q można pobrać z odczytów liczników linii.

Zatem strata napięcia w obwodzie elektrycznym zależy od:

• aktywny i reaktancja obwodu;

• składowe zastosowanej mocy;

• wielkość przyłożonego napięcia.

Wyprowadzenie wzorów do obliczania składowej poprzecznej spadku napięcia

Wróćmy do rysunku 7. Wartość wektora ac może być reprezentowana przez przeciwprostokątną trójkąta prostokątnego acd. Obliczyliśmy już stopę reklamową. Wyznaczmy składową poprzeczną cd.

Rysunek pokazuje, że cd = cf-df.

df = ce = ja ∙ R ∙ grzech φ.

cf = I ∙ x ∙ sałata φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Wykorzystując otrzymane modele wykonujemy małe przekształcenia matematyczne i uzyskujemy składową poprzeczną spadku napięcia.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Wyznaczanie wzoru do obliczania napięcia U1 na początku linii elektroenergetycznej

Znając wartość napięcia na końcu linii U2, stratę ∆Ul oraz składową poprzeczną spadku δU, możemy obliczyć wartość wektora U1 z twierdzenia Pitagorasa. W rozszerzonej formie ma następującą postać.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Praktyczne użycie

Obliczenia strat napięcia przeprowadzają inżynierowie na etapie tworzenia projektu obwodu elektrycznego w celu optymalnego doboru konfiguracji sieci i jej elementów składowych.

Podczas eksploatacji instalacji elektrycznych w razie potrzeby można okresowo przeprowadzać jednoczesne pomiary wektorów napięć na końcach linii i porównywać wyniki uzyskane metodą prostych obliczeń Metoda ta jest odpowiednia dla urządzeń o zwiększonej wymagania ze względu na konieczność dużej dokładności pracy.

Straty napięcia w obwodach wtórnych

Przykładem są obwody wtórne pomiarowych przekładników napięciowych, które czasami osiągają długość kilkuset metrów i są przesyłane specjalnym kablem zasilającym o zwiększonym przekroju.

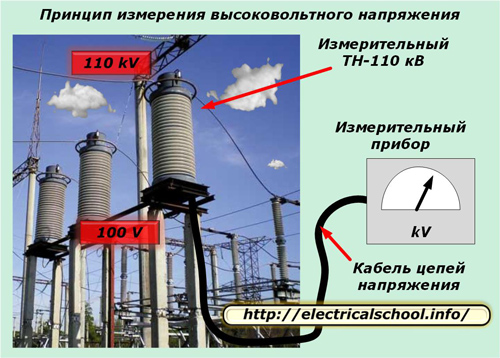
Charakterystyka elektryczna takiego kabla podlega zwiększonym wymaganiom dotyczącym jakości przenoszenia napięcia.

Współczesna ochrona urządzeń elektrycznych wymaga pracy układów pomiarowych o wysokich wskaźnikach metrologicznych i klasie dokładności 0,5 lub nawet 0,2. Dlatego straty przyłożonego do nich napięcia muszą być monitorowane i brane pod uwagę. W przeciwnym razie błąd wprowadzony przez nich do działania sprzętu może znacząco wpłynąć na wszystkie cechy operacyjne.

Straty napięcia w długich liniach kablowych

Cechą konstrukcji długiego kabla jest to, że ma on rezystancję pojemnościową ze względu na dość ciasne ułożenie rdzeni przewodzących i cienką warstwę izolacji między nimi. Ponadto odchyla wektor prądu przechodzący przez kabel i zmienia jego wielkość.

W obliczeniach zmiany wartości I ∙ z należy uwzględnić wpływ spadku napięcia na rezystancję pojemnościową. W przeciwnym razie opisana powyżej technologia nie ulegnie zmianie.

W artykule podano przykłady strat i spadków napięcia na napowietrznych liniach elektroenergetycznych i kablach. Można je jednak znaleźć we wszystkich odbiornikach energii elektrycznej, w tym w silnikach elektrycznych, transformatorach, cewkach indukcyjnych, bateriach kondensatorów i innych urządzeniach.

Wielkość strat napięciowych dla każdego rodzaju urządzeń elektrycznych jest prawnie uregulowana w zakresie warunków eksploatacji, a zasada ich wyznaczania we wszystkich obwodach elektrycznych jest taka sama.