Elektrony zachowują się jak fale

Fizycy od dawna wiedzą, że światło jest falą elektromagnetyczną. Do dziś nikt nie wątpi w to stanowisko, ponieważ światło wyraźnie wykazuje wszystkie oznaki zachowania się fal: fale świetlne mogą nakładać się na siebie, tworząc obraz interferencyjny, są też w stanie rozdzielać się, zaginając wokół przeszkód w czasie dyfrakcji.

Kiedy widzimy ptaka, który chodzi jak kaczka, pływa jak kaczka i kwacze jak kaczka, nazywamy go kaczką. Więc światło jest fala elektromagnetycznana podstawie obiektywnie zaobserwowanych oznak zachowania się takiej fali w świetle.

Jednak pod koniec XIX i XX wieku fizycy mieli zacząć mówić o „dualizmie cząstek i fal” światła. Okazuje się, że wiedza, że ​​światło jest falą elektromagnetyczną, to nie wszystko, co nauka wie o świetle. Naukowcy odkryli bardzo interesującą cechę światła.

Okazuje się, że w jakiś sposób światło manifestuje się jako zachowanie strumienia cząstek.Stwierdzono, że energia niesiona przez światło, po przeliczeniu przez określony czas przez specjalny detektor, okazuje się i tak złożona z pojedynczych (całych) kawałków.

Stało się zatem prawdą, że energia światła jest dyskretna, ponieważ składa się niejako z pojedynczych cząstek - „kwantów”, czyli z najmniejszych całych porcji energii. Taką cząstkę światła, niosącą jednostkę (lub kwant) energii, zaczęto nazywać fotonem.

Energię jednego fotonu oblicza się ze wzoru:

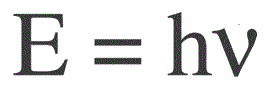
E — energia fotonu, h — stała Plancka, v — częstotliwość.

Niemiecki fizyk Max Planck jako pierwszy eksperymentalnie ustalił fakt nieciągłości fali świetlnej i obliczył wartość stałej h, która pojawia się we wzorze na znajdowanie energii poszczególnych fotonów. Ta wartość okazała się: 6,626 * 10-34 J * s. Planck opublikował wyniki swojej pracy pod koniec XX wieku.

Rozważmy na przykład fioletowy promień. Częstotliwość takiego światła (f lub v) wynosi 7,5 * 1014 Hz. Stała Plancka (h) wynosi 6,626 * 10-34 J * s. Oznacza to, że energia fotonu (E), charakterystyczna dla barwy fioletowej, wynosi 5*10-19 J. Jest to tak mała porcja energii, że bardzo trudno ją uchwycić.

Wyobraź sobie górski potok — płynie jako jedna całość i nie można zobaczyć gołym okiem, że tak naprawdę składa się on z pojedynczych cząsteczek wody. Dziś jednak wiemy, że obiekt makroskopowy – przepływ – jest właściwie dyskretny, to znaczy składa się z pojedynczych cząsteczek.

Oznacza to, że jeśli możemy umieścić licznik cząsteczek obok strumienia, aby zliczać cząsteczki wody przechodzące w miarę przepływu strumienia, detektor zawsze będzie zliczał tylko całkowite liczby cząsteczek wody, a nie częściowe.

Podobnie wykres całkowitej energii fotonu E, obliczony w czasie t — zawsze okaże się nie liniowy (żółta cyfra), ale schodkowy (zielona cyfra):

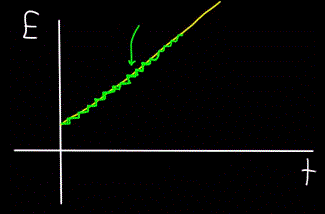
Tak więc fotony się poruszają, przenoszą energię, więc mają pęd. Ale foton nie ma masy. Jak w takim razie znaleźć rozpęd?

W rzeczywistości dla obiektów poruszających się z prędkościami bliskimi prędkości światła klasyczny wzór p = mv po prostu nie ma zastosowania. Aby zrozumieć, jak znaleźć pęd w tym niezwykłym przypadku, przejdźmy do szczególnej teorii względności:

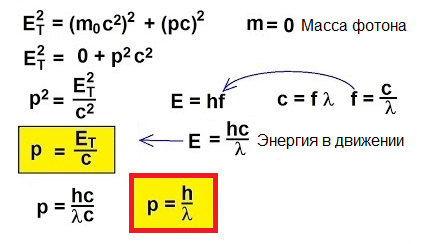
W 1905 roku Albert Einstein wyjaśnił z tego punktu widzenia efekt fotoelektryczny… Wiemy, że metalowa płytka zawiera w sobie elektrony, które są przyciągane przez dodatnio naładowane jądra atomów i dlatego są zatrzymywane w metalu. Ale jeśli poświecisz taką płytkę światłem o PEWNEJ częstotliwości, to możesz wybić elektrony z płytki.

To tak, jakby światło zachowywało się jak strumień cząstek z pędem i chociaż foton nie ma masy, to jednak w jakiś sposób oddziałuje z elektronem w metalu iw pewnych warunkach foton jest w stanie wybić elektron.

Jeśli więc foton padający na płytkę ma wystarczającą energię, to elektron zostanie wybijany z metalu i porusza się poza płytą z prędkością v. Taki wybity elektron nazywamy fotoelektronem.

Ponieważ wybity elektron ma znaną masę m, będzie miał pewną energię kinetyczną mv.

Energia fotonu, gdy działał na metal, zamienia się w energię wyjścia elektronu z metalu (funkcja wyjścia) i w energię kinetyczną elektronu, dzięki której wybijany elektron zaczyna się poruszać z metalu, pozostawiając go.

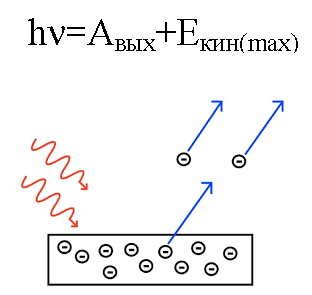
Załóżmy, że foton o znanej długości fali uderza w powierzchnię metalu, dla którego znana jest praca wyjściowa (elektronu z metalu). W tym przypadku łatwo można znaleźć energię kinetyczną elektronu emitowanego z danego metalu, a także jego prędkość.

Jeśli energia fotonu nie jest wystarczająca, aby elektron wykonał pracę wyjściową, to elektron po prostu nie może opuścić powierzchni danego metalu i fotoelektron nie powstaje.

W 1924 roku francuski fizyk Ludwik de Broglie przedstawić przełomowy pomysł, zgodnie z którym nie tylko fotony światła, ale same elektrony mogą zachowywać się jak fale. Naukowiec wyprowadził nawet wzór na hipotetyczną długość fali elektronu. Fale te nazwano później „falami de Broglie”.

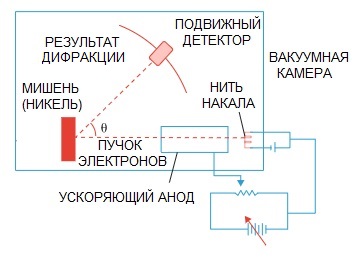
Hipoteza De Broglie została później potwierdzona. Eksperyment fizyczny dotyczący dyfrakcji elektronów, przeprowadzony w 1927 roku przez amerykańskich naukowców Clintona Davisona i Lestera Germera, ostatecznie wskazał na falową naturę elektronu.

Kiedy wiązka elektronów została skierowana przez specjalną strukturę atomową, wydaje się, że detektor powinien był zarejestrować obraz cząstek lecących jedna po drugiej, czego logicznie można by się spodziewać, gdyby elektrony były cząstkami.

Ale w praktyce mamy obraz charakterystyczny dla dyfrakcji fali. Co więcej, długości tych fal są całkowicie zgodne z koncepcją zaproponowaną przez de Broglie.

Ostatecznie pomysł de Broglie'a umożliwił wyjaśnienie zasady modelu atomowego Bohra, a później umożliwił Erwinowi Schrödingerowi uogólnienie tych pomysłów i położenie podwalin współczesnej fizyki kwantowej.