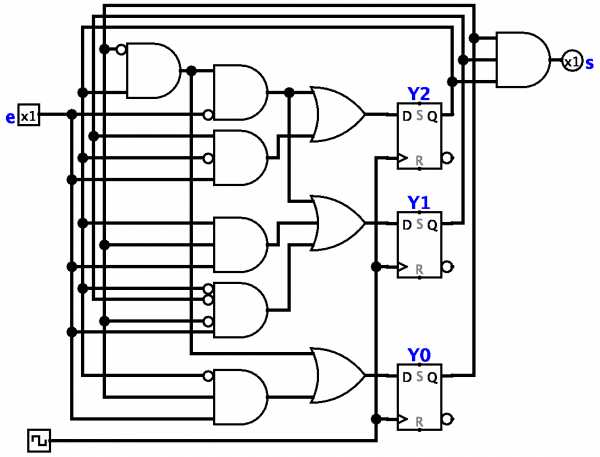
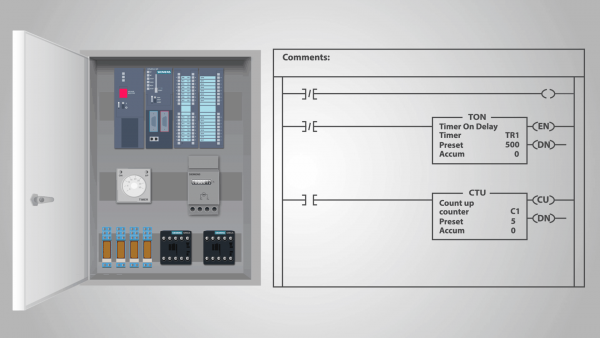
Teoria automatów, automaty skończone
Struktura, konstrukcja, zasada działania różnych maszyn są w dużej mierze zdeterminowane przez ich cel funkcjonalny. Rozróżnij maszyny technologiczne, transportowe, komputerowe, wojskowe i inne. Całe automatyczne kompleksy przeznaczone do wykonywania złożonych procesów technologicznych są szeroko wprowadzane w różnych gałęziach przemysłu. Zaprojektowano i zbudowano automaty, które wykonują różne funkcje logiczne (maszyny logiczne).
Teoria automatów — sekcja cybernetyki, które powstały pod wpływem wymagań technologii komputerów cyfrowych i maszyn sterujących. Dyskretne automaty badane w teorii automatów to abstrakcyjne modele rzeczywistych systemów (zarówno technicznych, jak i biologicznych), które przetwarzają dyskretne (cyfrowe) informacje w dyskretnych krokach czasowych.
Teoria automatów opiera się na precyzyjnych koncepcjach matematycznych, które formalizują intuicyjne wyobrażenia o funkcjonowaniu (zachowaniu) automatu oraz o jego strukturze (strukturze wewnętrznej).
W tym przypadku transformacja informacji jest zawsze rozumiana jako operacja przekształcająca wejściowe sekwencje złożone z liter z alfabetu wejściowego na wyjściowe sekwencje złożone z liter z wyjściowego alfabetu.
Szeroko stosowany jest aparat logiki matematycznej, algebry, teorii prawdopodobieństwa, kombinatoryki i teorii grafów.
Narastał problem z teorią automatów w niektórych jej częściach (strukturalna teoria automatów). z teorii obwodów przekaźnikowo-stykowych, która zaczęła kształtować się pod koniec lat 30. włącznie metody algebry logicznej.

W strukturalnej teorii automatów badane są różne typy schematów, mające na celu opisanie, w jaki sposób złożony automat jest tworzony z prostszych komponentów (elementów) odpowiednio połączonych w system.
Inny kierunek, zwany abstrakcyjną teorią automatów, badający zachowanie automatów (czyli naturę dokonywanych przez nie transformacji informacji), abstrahując od specyfiki ich wewnętrznej budowy, powstał w latach pięćdziesiątych XX wieku.
W ramach abstrakcyjnej teorii automatów treść pojęć „automat” i „maszyna” zasadniczo wyczerpuje się w standardowym opisie przetwarzania informacji, jakie przeprowadza automat. Taka transformacja może mieć charakter deterministyczny, ale może też mieć charakter probabilistyczny.
Najczęściej badane są maszyny deterministyczne (automaty), do których należą automaty skończone — główny przedmiot badań w teorii automatów.
Skończona maszyna stanów charakteryzuje się ograniczoną ilością pamięci (liczba stanów wewnętrznych) i jest definiowana za pomocą funkcji przejścia.Przy pewnej rozsądnej idealizacji wszystkie współczesne maszyny matematyczne, a nawet mózg, z punktu widzenia ich funkcjonowania, można uznać za automaty skończone.
Terminy „maszyna sekwencyjna”, „automat Milly'ego”, „automat Moore'a” są używane w literaturze (i nie przez wszystkich autorów jednolicie) jako synonimy terminu „automat skończony” lub w celu podkreślenia pewnych cech funkcji przejściowych skończonego automat.
Automaty z nieograniczoną pamięcią to maszyna Turinga zdolna do (potencjalnie) dowolnej wydajnej transformacji informacji. Koncepcja „maszyny Turinga” powstała wcześniej niż koncepcja „maszyny skończonej” i jest badana głównie w teorii algorytmów.
Teoria automatów abstrakcyjnych jest blisko spokrewniona ze znanymi teoriami algebraicznymi, np. z teorią półgrup. Z aplikacyjnego punktu widzenia interesujące są wyniki charakteryzujące transformację informacji w automacie pod względem wielkości pamięci.
Tak jest na przykład w problemach z eksperymentami na automatach (prace E.F. Moore'a itp.), gdzie taką czy inną informację o funkcjach przejściowych automatu lub o pojemności jego pamięci uzyskuje się z wyników eksperymenty.
Kolejnym zadaniem jest obliczenie okresów sekwencji wyjściowych na podstawie dostępnych informacji o wielkości pamięci automatu oraz okresów sekwencji wejściowych.
Ogromne znaczenie ma opracowanie metod minimalizowania pamięci maszyn skończonych i badanie ich zachowania w losowych środowiskach.
W teorii automatów abstrakcyjnych problem syntezy jest następujący.W pewnym wyraźnie sformalizowanym języku zapisano warunki zachowania projektowanego automatu (dla zdarzenia reprezentowanego w automacie). W takim przypadku konieczne jest opracowanie metod, które zgodnie z każdym pisemnym warunkiem:
1) dowiedzieć się, czy istnieje taka maszyna stanów, aby przetworzona przez nią informacja spełniała ten warunek;
2) jeśli tak, to konstruowane są funkcje przejścia takiej skończonej maszyny stanów lub szacowana jest wielkość jej pamięci.
Rozwiązanie zadania syntezy w takim sformułowaniu zakłada wstępne stworzenie dogodnego języka do zapisu warunków pracy automatu z wygodnymi algorytmami przejścia od zapisu do funkcji przechodnich.
W strukturalnej teorii automatów problem syntezy polega na skonstruowaniu łańcucha elementów danego typu, który realizuje automat skończony określony przez jego funkcje przejścia. W tym przypadku zwykle określają jakieś kryterium optymalności (na przykład minimalną liczbę elementów) i dążą do uzyskania optymalnego schematu.
Jak się później okazało, oznacza to, że niektóre metody i koncepcje opracowane wcześniej w odniesieniu do obwodów przekaźnikowo-stykowych mają zastosowanie do obwodów innego typu.
W związku z rozwojem technologii elektronicznych najbardziej rozpowszechnione są schematy elementów funkcjonalnych (sieci logiczne). Szczególnym przypadkiem sieci logicznych są abstrakcyjne sieci neuronowe, których elementy nazywane są neuronami.
Opracowano wiele metod syntezy, w zależności od rodzaju obwodów i transformacji informacji, dla których są przeznaczone (Synteza urządzeń przekaźnikowych).
Patrzeć -Minimalizacja obwodów kombinacyjnych, mapy Carnota, synteza obwodów
Maszyna stanów skończonych — model matematyczny układu sterowania o stałej (niezdolnej do zwiększania się podczas pracy) wielkości pamięci.
Koncepcja maszyny skończonej jest matematyczną abstrakcją, która charakteryzuje ogólną charakterystykę zestawu systemów sterowania (na przykład wielopętlowego przekaźnika). Wszystkie takie systemy mają wspólne cechy, które są naturalne do zaakceptowania jako definicja automatu skończonego.
Każdy skompletowany automat posiada wejście narażone na wpływy zewnętrzne oraz elementy wewnętrzne. Zarówno dla elementów wejściowych, jak i wewnętrznych istnieje stała liczba dyskretnych stanów, które mogą przyjmować.
Zmiana stanów elementów wejściowych i wewnętrznych następuje w dyskretnych momentach w czasie, których odstępy nazywane są tikami. Stan wewnętrzny (stan elementów wewnętrznych) na końcu taśmy jest całkowicie określony przez stan wewnętrzny i stan wejścia na początku taśmy.
Do tej cechy można sprowadzić wszystkie inne definicje automatu skończonego, w szczególności definicje, które zakładają, że automat skończony ma wyjście zależne od stanu wewnętrznego automatu w danej chwili.
Przy takiej charakterystyce charakter jego wejść i stanów wewnętrznych nie ma znaczenia dla opisu kompletnego automatu. Zamiast wejść i stanów, możesz po prostu spojrzeć na ich numery w losowej numeracji.
Maszyna stanowa zostanie ustawiona, jeżeli zostanie określona zależność jej numeru stanu wewnętrznego od poprzedniego numeru stanu wewnętrznego oraz numeru poprzedniego stanu wejścia. Takie zadanie może mieć formę stołu finałowego.
Innym powszechnym sposobem definiowania pełnego automatu jest konstrukcja tzw diagramy przejść. Stany wejściowe są często nazywane po prostu wejściami, a stany wewnętrzne to po prostu stany.
Maszyna stanów skończonych może być modelem zarówno urządzeń technicznych, jak i niektórych układów biologicznych. Automaty pierwszego typu to na przykład urządzenia przekaźnikowe i różne komputery elektroniczne, m.in. programowalne sterowniki logiczne.
W przypadku przekaźnika rolę stanów wejściowych pełnią kombinacje stanów czułych elementów przekaźnika (każda kombinacja takich stanów jest „stanem złożonym”, charakteryzującym się wskazaniem wszystkich czułych elementów te dyskretne stany jakie posiadają w danej chwili). Podobnie kombinacje stanów elementów pośrednich urządzenia przekaźnikowego działają jako stany wewnętrzne.
Programowalny sterownik logiczny (PLC) jest przykładem urządzenia przekaźnikowego, które można nazwać samodzielną maszyną stanową.
W rzeczywistości po wprowadzeniu programu do sterownika PLC i rozpoczęciu obliczeń przez sterownik, nie jest on narażony na wpływy zewnętrzne, a każdy kolejny stan jest całkowicie zdeterminowany stanem poprzednim. Możemy założyć, że wejście ma ten sam stan w każdym cyklu zegara.
I odwrotnie, każda skończona maszyna stanów, która ma jedyny możliwy stan wejściowy, jest naturalnie nazywana autonomiczną, ponieważ w tym przypadku środowisko zewnętrzne nie przenosi żadnych informacji kontrolujących jej zachowanie.
Zobacz też:
Wykorzystanie układów mikroprocesorowych w elektrotechnice na przykładzie zastosowania PLC