Wartości RMS prądu i napięcia
Przemienny prąd sinusoidalny ma różne wartości chwilowe w tym okresie. Naturalne jest pytanie, jaką wartość prądu zmierzymy amperomierzem zawartym w obwodzie?
Podczas obliczania obwodów prądu przemiennego, a także pomiarów elektrycznych, niewygodne jest stosowanie wartości chwilowych lub amplitudowych prądów i napięć, a ich średnie wartości w okresie wynoszą zero. Ponadto efekt elektryczny okresowo zmieniającego się prądu (ilość wydzielanego ciepła, idealne działanie itp.) Nie może być oszacowany na podstawie amplitudy tego prądu.
Najwygodniejsze było wprowadzenie koncepcji tak zwanych skutecznych wartości prądu i napięcia... Pojęcia te opierają się na termicznym (lub mechanicznym) działaniu prądu, który nie zależy od jego kierunku.
Wartość pierwiastkowa prądu przemiennego - jest to wartość prądu stałego, przy której w okresie prądu przemiennego wydziela się w przewodniku taka sama ilość ciepła, jak przy prądzie przemiennym.
Aby ocenić podjęte działania prąd przemienny, porównamy jego działanie z efektem termicznym prądu stałego.
Moc prądu stałego P A przechodząca przez rezystancję r będzie wynosić P = P2r.
Moc prądu przemiennego wyraża się jako średni efekt mocy chwilowej Az2r w całym okresie lub jako średnią (I am x sinωT)2 NS r w tym samym czasie.
Niech średnia wartość t2 dla okresu będzie równa M. Przyrównując moc prądu stałego i moc prądu przemiennego, mamy: Az2r = Mr -n, skąd Az = √M,
Wielkość I nazywana jest wartością skuteczną prądu przemiennego.
Średnią wartość i2 przy prądzie przemiennym określa się w następujący sposób.
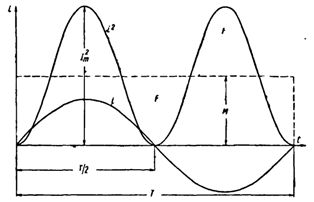
Skonstruujmy sinusoidalną krzywą prądu. Podnosząc do kwadratu każdą chwilową wartość prądu, otrzymujemy krzywą P w funkcji czasu.
Wartość skuteczna AC
Obie połowy tej krzywej leżą powyżej osi poziomej, ponieważ prądy ujemne (-i) w drugiej połowie okresu, po podniesieniu do kwadratu, dają wartości dodatnie.
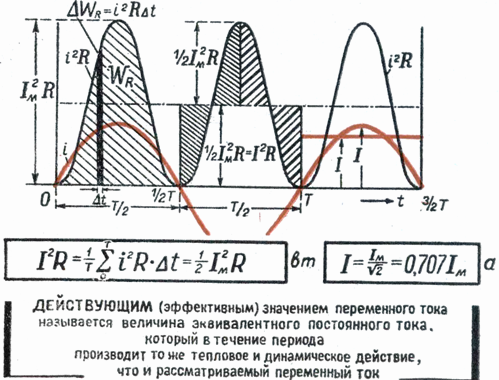
Skonstruuj prostokąt o podstawie T i polu równym polu ograniczonemu krzywą i2 i osią poziomą. Wysokość prostokąta M będzie odpowiadać średniej wartości P dla okresu. Ta wartość okresu, obliczona za pomocą wyższej matematyki, będzie równa 1/2 I2m... Zatem M. = 1/2 I2m
Ponieważ wartość skuteczna Im prąd przemienny wynosi Im = √Mnastępnie I = Im / √2
Podobnie zależność pomiędzy wartościami skutecznymi i amplitudowymi dla napięć U i E ma postać:
U = Um / √2E = Em / √2
Efektywne wartości zmiennych są oznaczone dużymi literami bez indeksów dolnych (I, U, E).
Na podstawie powyższego możemy powiedzieć, że wartość skuteczna prądu przemiennego jest równa takiemu prądowi stałemu, który przechodząc przez ten sam opór co prąd przemienny, uwalnia w tym samym czasie taką samą ilość energii.
Elektryczne przyrządy pomiarowe (amperomierze, woltomierze) zawarte w obwodzie prądu przemiennego wskazują skuteczne wartości prądu lub napięcia.
Podczas konstruowania diagramów wektorowych wygodniej jest odłożyć nie amplitudę, ale efektywne wartości wektorów. W tym celu długości wektorów zmniejszamy raz o √2. Nie zmienia to położenia wektorów na diagramie.