Efekt powierzchniowy i efekt bliskości

Rezystancję przewodnika na prąd stały określa dobrze znany wzór ro = ρl / S.

Rezystancję tę można również wyznaczyć, znając wielkość stałego prądu IО i mocy PO:

ro = PO / AzO2

Okazuje się, że w obwodzie prądu przemiennego rezystancja r tego samego przewodnika jest większa niż rezystancja prądu stałego: r> rО

Ta rezystancja r w przeciwieństwie do rezystancji prądu stałego rO i nazywana jest rezystancją czynną. Wzrost rezystancji drutu tłumaczy się tym, że przy prądzie przemiennym gęstość prądu nie jest taka sama w różnych punktach przekroju drutu. Mam powierzchnie przewodników, gęstość prądu jest większa niż przy prądzie stałym, a środek jest mniejszy.

Przy wysokiej częstotliwości nieregularności pojawiają się tak gwałtownie, że gęstość prądu w znacznej centralnej czystości przekroju przewodnika jest praktycznie zerowa. Prąd przepływa tylko w warstwie powierzchniowej, dlatego zjawisko to nazywane jest efektem powierzchniowym.

Efekt powierzchniowy prowadzi zatem do zmniejszenia przekroju przewodnika, przez który przepływa prąd (przekrój czynny), a tym samym do wzrostu jego rezystancji w stosunku do rezystancji prądu stałego.

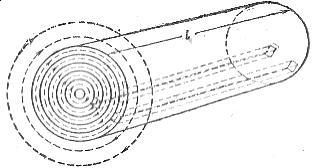
Aby wyjaśnić przyczynę efektu powierzchniowego, wyobraź sobie cylindryczny przewodnik (rys. 1), składający się z dużej liczby elementarnych przewodników o tym samym przekroju, znajdujących się blisko siebie i ułożonych w koncentryczne warstwy.

Rezystancje tych drutów na prąd stały, określone wzorem ρl / S, będą takie same.

Ryż. 1. Pole magnetyczne przewodnika cylindrycznego.

Zmienny prąd elektryczny wytwarza zmienne pole magnetyczne wokół każdego drutu (ryc. 1). Oczywiście elementarny przewodnik znajdujący się bliżej osi jest otoczony przewodem powierzchniowym o dużym strumieniu magnetycznym, dlatego ten pierwszy ma większą indukcyjność i reaktancję indukcyjną niż ten drugi.

Przy tym samym napięciu na końcach elementarnych drutów o długości l, położonych wzdłuż osi i na powierzchni, gęstość prądu w pierwszym jest mniejsza niż w drugim.

Różnica v gęstość prądu wzdłuż osi i wzdłuż obwodu przewodnika wzrasta wraz ze wzrostem średnicy przewodnika d, przewodnictwa materiału γ, przenikalności magnetycznej materiału μ i częstotliwości prądu przemiennego.

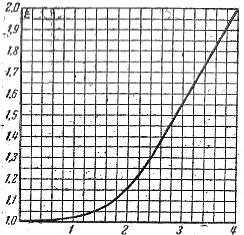
Stosunek czynnej rezystancji przewodnika r do jego rezystancji w. prąd stały rО nazywany jest współczynnikiem efektu naskórkowości i jest oznaczony literą ξ (xi), dlatego współczynnik ξ można wyznaczyć z wykresu na ryc. 2, który pokazuje zależność ξ od iloczynu d i √γμμое.

Ryż. 2. Wykres do wyznaczania współczynnika efektu naskórkowości.

Przy obliczaniu tego iloczynu d należy wyrazić w cm, γ — w 1/om-cm, μo — v gn/ cm, a f = w Hz.

Przykład. Konieczne jest wyznaczenie współczynnika efektu naskórkowości dla I am przewodnika miedzianego o średnicy d= 11,3 mm (S = 100 mm2) przy częstotliwości f = 150 Hz.

Dobra robota.

Zgodnie z wykresem na ryc. 2 znajdujemy ξ = 1,03

Nierówna gęstość prądu w przewodniku występuje również na skutek wpływu prądów w sąsiednich przewodach. Zjawisko to nazywane jest efektem bliskości.

Rozważając pole magnetyczne prądów o tym samym kierunku w dwóch równoległych przewodnikach, łatwo wykazać, że te elementarne przewodniki należące do różnych przewodników, które są najbardziej oddalone od siebie, są połączone najmniejszym strumieniem magnetycznym, stąd gęstość prądu w nich jest najwyższy. Jeśli prądy w równoległych przewodach mają różne kierunki, można wykazać, że obserwuje się dużą gęstość prądu w tych elementarnych przewodach należących do różnych drutów, które są najbliżej siebie.