Prawo zachowania energii

Współczesna fizyka zna wiele rodzajów energii związanych z ruchem lub różnymi wzajemnymi układami różnych ciał materialnych lub cząstek, na przykład każde poruszające się ciało ma energię kinetyczną proporcjonalną do kwadratu jego prędkości. Ta energia może się zmienić, jeśli prędkość ciała wzrośnie lub spadnie. Ciało uniesione nad ziemię ma energię potencjalną grawitacji zmieniającą trzy zmiany wysokości ciała.

Stacjonarne ładunki elektryczne znajdujące się w pewnej odległości od siebie mają elektrostatyczną energię potencjalną zgodnie z faktem, że zgodnie z prawem Coulomba ładunki albo się przyciągają (jeśli mają różne znaki), albo odpychają się z siłą odwrotnie proporcjonalną do kwadratu odległość między nimi.

Energię kinetyczną i potencjalną posiadają cząsteczki, atomy i cząstki, ich składniki — elektrony, protony, neutrony itp. w postaci pracy mechanicznej, w przepływie prądu elektrycznego, w przekazywaniu ciepła, w zmianie stanu wewnętrznego ciał, w propagacji fal elektromagnetycznych itp.

Ponad 100 lat temu ustanowiono fundamentalne prawo fizyki, zgodnie z którym energia nie może zniknąć ani powstać z niczego. Ona może tylko zmienić jeden typ na inny…. To prawo nazywa się prawem zachowania energii.

W pracach A. Einsteina prawo to jest znacznie rozwinięte. Einstein ustalił zamienność energii i masy, a tym samym rozszerzył interpretację prawa zachowania energii, które jest obecnie powszechnie określane jako prawo zachowania energii i masy.

Zgodnie z teorią Einsteina każda zmiana energii ciała dE jest powiązana ze zmianą jego masy dm wzorem dE = dmc2, gdzie c jest prędkością światła w próżni równą 3 x 108 Miss.

W szczególności z tego wzoru wynika, że ​​jeżeli w wyniku jakiegoś procesu masa wszystkich ciał biorących udział w tym procesie zmniejszy się o 1 g, to energia równa się 9⋅1013 J, co odpowiada 3000 ton standardowe paliwo.

Stosunki te mają pierwszorzędne znaczenie w analizie przemian jądrowych. W większości procesów makroskopowych zmianę masy można pominąć i można mówić jedynie o prawie zachowania energii.

Prześledźmy przemiany energii na jakimś konkretnym przykładzie. Rozważ cały łańcuch przemian energii wymaganych do wyprodukowania dowolnej części na tokarce (ryc. 1). Niech początkowa energia 1, której ilość przyjmujemy jako 100%, uzyskujemy w wyniku całkowitego spalenia pewnej ilości paliwa kopalnego. Dlatego dla naszego przykładu 100% energii początkowej zawarte jest w produktach spalania paliwa, które mają wysoką (około 2000 K) temperaturę.

Produkty spalania w kotle elektrowni po schłodzeniu oddają swoją energię wewnętrzną w postaci ciepła wodzie i parze wodnej. Jednak ze względów technicznych i ekonomicznych produktów spalania nie można schłodzić do temperatury otoczenia. Są wyrzucane przez rurkę do atmosfery w temperaturze około 400 K, zabierając ze sobą część pierwotnej energii. Dlatego tylko 95% energii początkowej zostanie przeniesione na energię wewnętrzną pary wodnej.

Powstała para wodna trafi do turbiny parowej, gdzie jej energia wewnętrzna jest początkowo częściowo zamieniana na energię kinetyczną strun parowych, która następnie zostanie przekazana jako energia mechaniczna do wirnika turbiny.

Tylko część energii pary może zostać przekształcona w energię mechaniczną. Pozostała część jest przekazywana do wody chłodzącej, gdy para wodna skrapla się w skraplaczu. W naszym przykładzie przyjęliśmy, że energia przekazywana do wirnika turbiny wyniesie około 38%, co w przybliżeniu odpowiada stanowi w nowoczesnych elektrowniach.

Przy zamianie energii mechanicznej na energię elektryczną w wyniku tzw Straty Joule'a w uzwojeniach wirnika i stojana generatora spowodują utratę około 2% energii. W rezultacie około 36% energii początkowej trafi do sieci.

Silnik elektryczny zamienia tylko część dostarczanej mu energii elektrycznej na energię mechaniczną potrzebną do obracania tokarki. W naszym przykładzie około 9% energii w postaci ciepła Joule'a w uzwojeniach silnika i ciepła tarcia w jego łożyskach zostanie uwolnione do otaczającej atmosfery.

Zatem tylko 27% energii początkowej zostanie dostarczone do organów roboczych maszyny. Ale wpadki energetyczne na tym się nie kończą. Okazuje się, że większość energii podczas obróbki części zużywana jest na tarcie iw postaci ciepła jest odprowadzana wraz z cieczą chłodzącą część. Teoretycznie tylko bardzo mały ułamek (w naszym przykładzie przyjmuje się 2%) początkowej energii wystarczyłby do uzyskania pożądanej części oryginalnej części.

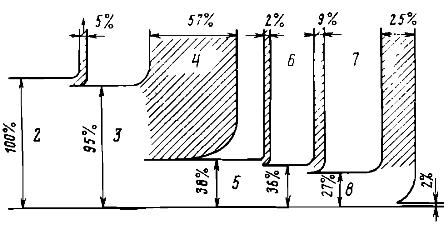
Ryż. 1. Schemat przemian energetycznych podczas obróbki przedmiotu na tokarce: 1 — strata energii ze spalinami, 2 — energia wewnętrzna produktów spalania, 3 — energia wewnętrzna płynu roboczego — pary wodnej, 4 — ciepło wydzielane z chłodzenia woda w skraplaczu turbiny, 5 — energia mechaniczna wirnika turbogeneratora, 6 — straty w generatorze elektrycznym, 7 — odpady w napędzie elektrycznym maszyny, 8 — energia mechaniczna obrotu maszyny, 9 — tarcie praca, która jest zamieniana na ciepło, oddzielone od cieczy, części chłodzącej, 10 — zwiększenie energii wewnętrznej części i wiórów po obróbce ...

Z rozważanego przykładu można wyciągnąć co najmniej trzy bardzo przydatne wnioski, jeśli uznamy go za dość typowy.

Po pierwsze, na każdym etapie przemiany energii część energii jest tracona... Stwierdzenia tego nie należy rozumieć jako naruszenia zasady zachowania energii. Jest tracone z powodu użytecznego efektu, dla którego przeprowadzana jest odpowiednia transformacja. Całkowita ilość energii po konwersji pozostaje niezmieniona.

Jeżeli proces przetwarzania i przekazywania energii odbywa się w określonej maszynie lub aparacie, to sprawność tego urządzenia zwykle charakteryzuje się sprawnością (sprawnością)... Schemat takiego urządzenia pokazano na ryc. 2.

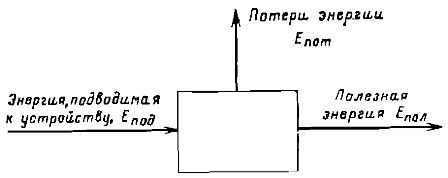
Ryż. 2. Schemat wyznaczania sprawności urządzenia przetwarzającego energię.

Korzystając z notacji pokazanej na rysunku, sprawność można zdefiniować jako Sprawność = Epol/Epod

Oczywiste jest, że w tym przypadku, w oparciu o prawo zachowania energii, musi istnieć Epod = Epol + Epot

Sprawność można zatem zapisać również w następujący sposób: sprawność = 1 — (Epot / Epol)

Wracając do przykładu pokazanego na FIG. 1, możemy powiedzieć, że sprawność kotła wynosi 95%, sprawność zamiany energii wewnętrznej pary na pracę mechaniczną wynosi 40%, sprawność generatora elektrycznego wynosi 95%, sprawność — napęd elektryczny maszyna — 75%, a wydajność rzeczywistej obróbki przedmiotu obrabianego wynosi około 7%.

W przeszłości, kiedy nie znano jeszcze praw przemiany energii, marzeniem ludzi było stworzenie tzw. perpetuum mobile — urządzenia, które wykonywałoby użyteczną pracę bez wydawania energii. Taki hipotetyczny silnik, którego istnienie naruszałoby zasadę zachowania energii, nazywa się dziś perpetuum mobile pierwszego rodzaju, w przeciwieństwie do perpetuum mobile drugiego rodzaju. poważnie możliwość stworzenia perpetuum mobile pierwszego rodzaju.

Po drugie, wszystkie straty energii są ostatecznie przekształcane w ciepło, które jest uwalniane albo do powietrza atmosferycznego, albo do wody z naturalnych zbiorników.

Po trzecie, ludzie zużywają tylko niewielką część energii pierwotnej, która jest wydatkowana w celu uzyskania odpowiedniego korzystnego efektu.

Jest to szczególnie widoczne, gdy przyjrzymy się kosztom transportu energii. W wyidealizowanej mechanice, która nie uwzględnia sił tarcia, przemieszczanie ładunków w płaszczyźnie poziomej nie wymaga energii.

W rzeczywistych warunkach cała energia zużywana przez pojazd jest wykorzystywana do pokonania sił tarcia i sił oporu powietrza, czyli ostatecznie cała energia zużywana w transporcie jest zamieniana na ciepło. W związku z tym interesujące są następujące liczby, charakteryzujące pracę przemieszczania 1 tony ładunku na odległość 1 km przy różnych rodzajach transportu: samolot — 7,6 kWh / (t-km), samochód — 0,51 kWh / ( t- km), pociągiem – 0,12 kWh/(t-km).

Tym samym ten sam korzystny efekt można osiągnąć transportem lotniczym kosztem 60-krotnie większej energochłonności niż koleją. Oczywiście duże zużycie energii daje znaczną oszczędność czasu, ale nawet przy tej samej prędkości (samochód i pociąg) koszty energii różnią się 4-krotnie.

Ten przykład sugeruje, że ludzie często idą na kompromis z efektywnością energetyczną, aby osiągnąć inne cele, na przykład wygodę, szybkość itp. Z reguły efektywność energetyczna samego procesu nas nie interesuje — ogólne kwestie techniczne i ekonomiczna ocena efektywności procesów jest ważna... Ale wraz ze wzrostem cen składników energii pierwotnej, składnik energetyczny w ocenach techniczno-ekonomicznych staje się coraz ważniejszy.