Elektron w polu elektrycznym

Ruch elektronu w polu elektrycznym jest jednym z najważniejszych procesów fizycznych w elektrotechnice. rysunek Zobaczmy, jak to się dzieje w próżni. Rozważmy najpierw przykład ruchu elektronu od katody do anody w jednorodnym polu elektrycznym.

Poniższy rysunek przedstawia sytuację, w której elektron opuszcza elektrodę ujemną (katodę) z pomijalnie małą prędkością początkową (zbliżającą się do zera) i wchodzi w jednolitym polu elektrycznymwystępuje między dwiema elektrodami.

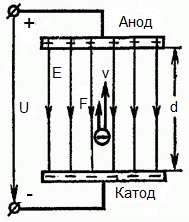
Do elektrod przyłożone jest stałe napięcie U, a pole elektryczne ma odpowiednią siłę E. Odległość między elektrodami jest równa d. W tym przypadku siła F będzie działać na elektron od strony pola, która jest proporcjonalna do ładunku elektronu i natężenia pola:

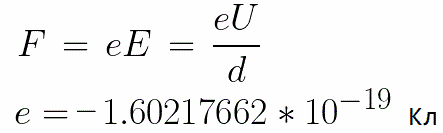
Ponieważ elektron ma ładunek ujemny, siła ta będzie skierowana przeciwko wektorowi natężenia pola E. Odpowiednio, elektron będzie przyspieszany w tym kierunku przez pole elektryczne.

Przyspieszenie, jakiego doświadcza elektron, jest proporcjonalne do wielkości działającej na niego siły F i odwrotnie proporcjonalne do masy elektronu m.Ponieważ pole jest jednorodne, przyspieszenie dla danego obrazu można wyrazić wzorem:

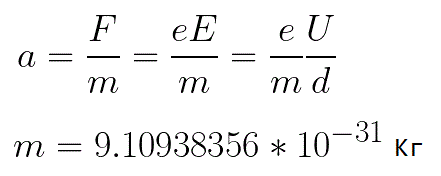
W tym wzorze stosunek ładunku elektronu do jego masy to ładunek właściwy elektronu, wielkość będąca stałą fizyczną:

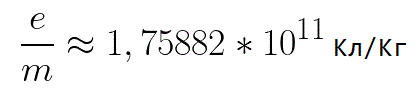
Zatem elektron znajduje się w przyspieszającym polu elektrycznym, ponieważ kierunek prędkości początkowej v0 pokrywa się z kierunkiem siły F działającej na bok pola, a zatem elektron porusza się ruchem jednostajnym. Jeśli nie ma przeszkód, przebędzie drogę d między elektrodami i dotrze do anody (elektrody dodatniej) z określoną prędkością v. W momencie, gdy elektron dotrze do anody, jego energia kinetyczna będzie odpowiednio równa:

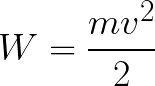
Ponieważ na całej drodze d elektron jest przyspieszany siłami pola elektrycznego, uzyskuje tę energię kinetyczną w wyniku pracy wykonanej przez siłę działającą na bok pola. Ta praca jest równa:

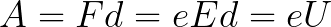
Wtedy energię kinetyczną uzyskaną przez elektron poruszający się w polu można znaleźć w następujący sposób:

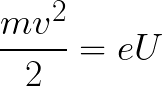
Oznacza to, że jest to nic innego jak praca sił pola w celu przyspieszenia elektronu między punktami o różnicy potencjałów U.

W takich sytuacjach, aby wyrazić energię elektronu, wygodnie jest użyć takiej jednostki miary, jak „elektronowolt”, która jest równa energii elektronu przy napięciu 1 wolta. A ponieważ ładunek elektronu jest stały, to 1 elektrowolt jest również wartością stałą:

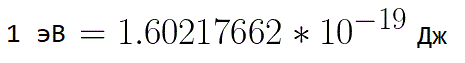
Z poprzedniego wzoru możesz łatwo określić prędkość elektronu w dowolnym punkcie jego ścieżki podczas poruszania się w przyspieszającym polu elektrycznym, znając tylko różnicę potencjałów, którą minął podczas przyspieszania:

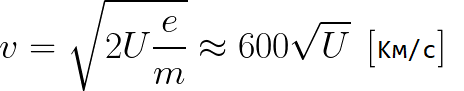
Jak widać, prędkość elektronu w przyspieszającym polu zależy tylko od różnicy potencjałów U między punktem końcowym i początkowym jego toru.

Wyobraź sobie, że elektron zaczyna oddalać się od katody z pomijalną prędkością, a napięcie między katodą a anodą wynosi 400 woltów. W tym przypadku w momencie dotarcia do anody jej prędkość będzie równa:

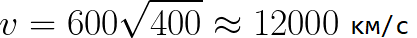
Łatwo jest również określić czas potrzebny elektronowi na pokonanie odległości d między elektrodami. Przy ruchu jednostajnie przyspieszonym ze stanu spoczynku prędkość średnia jest równa połowie prędkości końcowej, a czas przyspieszonego lotu w polu elektrycznym będzie równy:

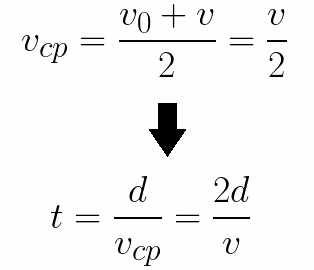
Rozważmy teraz przykład, w którym elektron porusza się w spowalniającym jednorodnym polu elektrycznym, to znaczy pole jest skierowane jak poprzednio, ale elektron zaczyna poruszać się w przeciwnym kierunku — od anody do katody.

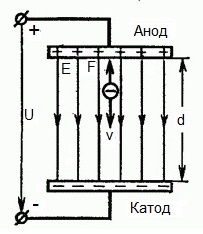
Załóżmy, że elektron opuścił anodę z pewną prędkością początkową v i początkowo zaczął poruszać się w kierunku katody. W tym przypadku siła F działająca na elektron od strony pola elektrycznego będzie skierowana przeciwnie do wektora natężenia elektrycznego E — od katody do anody.

Zacznie zmniejszać początkową prędkość elektronu, to znaczy pole będzie spowalniać elektron. Oznacza to, że w tych warunkach elektron zacznie się poruszać jednostajnie i jednostajnie wolno. Sytuacja jest opisana w następujący sposób: „elektron porusza się w spowalniającym polu elektrycznym”.

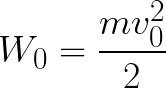
Z anody elektron zaczął się poruszać z niezerową energią kinetyczną, która zaczyna się zmniejszać podczas hamowania, ponieważ energia ta jest teraz wydatkowana na pokonanie siły działającej z pola na elektron.

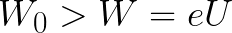
Gdyby początkowa energia kinetyczna elektronu opuszczającego anodę była natychmiast większa niż energia, którą musi wydać pole, aby przyspieszyć elektron podczas przemieszczania się z katody do anody (jak w pierwszym przykładzie), to elektron byłby pokona odległość d i ostatecznie dotrze do katody pomimo hamowania.

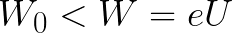
Jeśli początkowa energia kinetyczna elektronu jest mniejsza niż ta wartość krytyczna, elektron nie dotrze do katody. W pewnym momencie zatrzyma się, a następnie rozpocznie jednostajnie przyspieszony ruch z powrotem do anody. W rezultacie pole zwróci mu energię, która została zużyta w procesie zatrzymania.

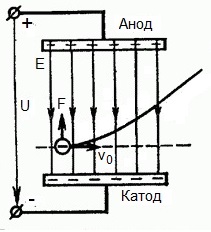
Ale co jeśli elektron leci z prędkością v0 w obszarze działania pola elektrycznego pod kątem prostym? Oczywiście siła działająca na stronę pola w tym obszarze jest skierowana na elektron od katody do anody, czyli przeciwnie do wektora natężenia pola elektrycznego E.

Oznacza to, że teraz elektron ma dwie składowe ruchu: pierwszą — z prędkością v0 prostopadłą do pola, drugą — jednostajnie przyspieszoną pod działaniem siły od strony pola skierowanej w stronę anody.

Okazuje się, że elektron, wlatując w pole działania, porusza się po trajektorii parabolicznej. Ale po wylocie z obszaru działania pola elektron będzie kontynuował swój jednostajny ruch bezwładności po trajektorii linii prostej.