Obliczanie potencjometru i bocznika złożonego

Pojęcia i formuły

Potencjometr to zmienna rezystancja z suwakiem, który jest zawarty, jak pokazano na ryc.

Aby uzyskać więcej informacji, patrz — Potencjometry i ich zastosowania

Do punktów 1 i 2 przykłada się napięcie U. Z punktów 2 i 3 usuwa się regulowane napięcie, którego wartość jest mniejsza od U i zależy od położenia suwaka. Dzielniki napięcia mają podobny schemat, ale nie są regulowane i nie mają ruchomego suwaka.

Potencjometry, dzielniki napięcia i złożone boczniki są obliczane za pomocą Prawa Kirchhoffa, takich jak obliczanie konwencjonalnych obwodów z rezystancjami.

Przykłady

1. Napięcie źródła wynosi U = 24 V, całkowita rezystancja potencjometru wynosi r = 300 Ohm. Silnik jest montowany oddzielnie, tak aby r1 = 50 omów. Jakie napięcie U1 można usunąć z punktów 3 i 2 (rys. 1)?

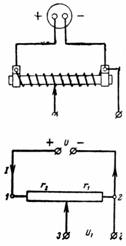
Ryż. 1.

Prąd I i napięcie U na rezystancji r są powiązane wzorem I ∙ r = U.

Suwak potencjometru oddziela część rezystancji tj. opór r1. Spadek napięcia między punktami 3 i 2 jest równy I ∙ r1 = U1.

Ze stosunku spadku napięcia otrzymujemy równość (I ∙ r1) / (I ∙ r) = U1 / U. Im większa rezystancja r1, tym większa wartość napięcia U1 między punktami 3 i 2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. Potencjometr (rys. 2) jest obciążony na żarówce o rezystancji r = 100 omów. Potencjometr podzielony jest suwakiem na dwie części o oporności r1 = 600 Ohm i r2 = 200 Ohm. Wyznacz napięcie Ul i prąd lampy Il.

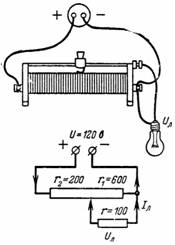
Ryż. 2.

Prąd I płynie przez rezystancję r2, a prąd Il przepływa przez lampę. Przez rezystancję r1 przepływa prąd I-Il, który wytwarza na rezystancji r1 napięcie równe napięciu lampy: (I-Il) ∙ r1 = Ul.

Z drugiej strony napięcie lampy jest równe napięciu źródła minus spadek napięcia przy rezystancji r2: U-I ∙ r2 = Ul.

Prąd I jest równy napięciu źródła podzielonemu przez wynikową rezystancję szeregowo-równoległego połączenia rezystancji:

ja = U / (r2 + (r ∙ r1) / (r + r1)).

Podstawiamy wyrażenie na całkowity prąd źródła w drugim równaniu:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Po przekształceniu otrzymujemy wyrażenie na napięcie lampy:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Jeśli przekształcimy to wyrażenie, wychodząc z faktu, że Ul = Il ∙ r, to otrzymamy wyrażenie na prąd lampy:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Zastąp wartości liczbowe w wynikowych równaniach:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul / r = 36/100 = 0,36 A.

3. Oblicz napięcie Up i prąd Ip przyrządu pomiarowego podłączonego do części potencjometru. Urządzenie ma rezystancję r = 1000 omów. Punkt rozgałęzienia dzieli rezystancję dzielnika na r2 = 500 omów i r1 = 7000 omów (rys. 3).Napięcie na zaciskach potencjometru U = 220 V.

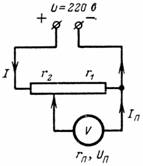
Ryż. 3.

Korzystając z otrzymanych wcześniej wzorów, możemy napisać, że prąd płynący przez urządzenie wynosi:

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙ 1000)= 1540000/11000000 = 1,54 / 11 = 0,14A.

Up = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Oblicz napięcie urządzenia Up, jeśli pobiera ono prąd Ip = 20 mA i jest podłączone do potencjometru podzielonego na rezystancje r2 = 10 ^ 4 Ohm i r1 = 2 ∙ 10 ^ 4 Ohm (rys. 3).

Całkowite napięcie w dzielniku napięcia jest równe sumie spadków napięć w jego częściach (przez rezystancje r1 i r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + Góra

Prąd źródła jest rozgałęziony w punkcie styku silnika: I = I1 + Ip; I = Upn / r1 + In.

Podstawiamy wartość prądu I do równania napięciowego:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Zatem napięcie urządzenia Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Zastąp wartości liczbowe: Up = (220-0,02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13,3 V.

5. Źródło prądu stałego o napięciu U = 120 V zasila obwody anodowe odbiornika radiowego poprzez potencjometr (dzielnik napięcia), który wraz z filtrem ma rezystancję r = 10000 Ohm. Napięcie U1 jest usuwane przez rezystancję r2 = 8000 Ohm. Oblicz napięcie anodowe bez obciążenia i przy prądzie obciążenia I = 0,02 A (rys. 4).

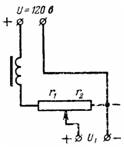
Ryż. 4.

Pierwszy przypadek jest podobny do przykładu 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

Drugi przypadek jest podobny do przykładu 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Podczas ładowania napięcie spadnie z 96 do 64 V.Jeśli potrzebne jest większe napięcie, należy przesunąć suwak w lewo, czyli zwiększyć rezystancję r2.

6. Napięcia Ua i Ub są usuwane przez dzielnik napięcia. Całkowita rezystancja dzielnika napięcia podłączonego do napięcia U1 = 220 V wynosi r = 20 000 omów. Jakie jest napięcie Ua w rezystancji r3 = 12000 omów przy poborze prądu Ia = 0,01 A oraz napięcie Ub w rezystancji r2 + r3 = 18000 omów przy poborze prądu Ib = 0,02 A (rys. 5).

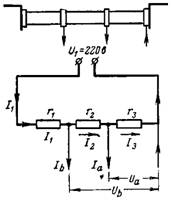
Ryż. 5.

Rezystancja napięciowa r3

Ua = I3 ∙ r3;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

Napięcie Ub jest równe sumie spadku napięcia Ua na rezystancji r3 i spadku napięcia na rezystancji r2. Spadek napięcia na rezystancji r2 jest równy I2 ∙ r2. Prąd I2 = Ia + I3. Prąd I3 można obliczyć jak w przykładzie 1:

I3 = (220-80-40) / 20 000 = 0,005 A;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Napięcie Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

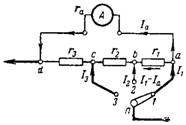
7. Oblicz bocznik złożony dla miliamperomierza tak, aby przy różnych położeniach przełącznika miał następujące zakresy pomiarowe: I1 = 10 mA; I2 = 30mA; I3 = 100mA. Schemat połączenia bocznika pokazano na ryc. 6. Rezystancja wewnętrzna urządzenia ra = 40 Ohm. Wewnętrzny zakres pomiarowy miliamperomierza 2 mA.

Ryż. 6.

Podczas pomiaru prądu I≤2mA bocznik jest wyłączony.

a) Podczas pomiaru prądu I = 10 mA przełącznik znajduje się w pozycji 1, a prąd 10-2 = 8 mA przepływa przez wszystkie rezystancje bocznika. Spadek napięcia na rezystancji bocznika Ush i urządzeniu Ua między punktami d i a musi być taki sam

Usz = Ua;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Przy pomiarze prądu I2 = 30 mA przełącznik znajduje się w pozycji 2. Zmierzony prąd podzieli się w punkcie b. Przy pełnym odchyleniu wskazówki urządzenia prąd Ia = 2 mA przepłynie przez rezystancję r1 i urządzenie ra.

Reszta prądu I2-Ia przejdzie przez rezystancje r2 i r3. Prądy spowodują taki sam spadek napięcia na dwóch gałęziach między punktami d i b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) W podobny sposób obliczenia wykonamy przy zwiększeniu zakresu pomiarowego do I3 = 100 mA. Prąd I3-Ia popłynie przez rezystancję r3, a prąd Ia przez rezystancje r1, r2, ra. Napięcie w obu gałęziach jest takie samo: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

Otrzymaliśmy trzy równania z trzema nieznanymi wartościami rezystancji r1, r2 i r3.

Mnożymy wszystkie równania przez 1000 i konwertujemy je:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -r1 = 40;

49 ∙ r3-r1-r2 = 40.

Dodajmy pierwsze i trzecie równanie: 50 ∙ r3 = 50;

r3 = 50/50 = 1 om.

Dodajmy pierwsze i drugie równanie: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2,34 oma.

Podstawmy otrzymane wyniki do pierwszego równania: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6,66 oma.

Poprawność obliczeń można sprawdzić podstawiając otrzymane wartości rezystancji do równań.