Wytrzymałość dielektryczna izolacji. Przykłady obliczeń

Wraz ze stopniowym wzrostem napięcia U między przewodami oddzielonymi dielektrykiem (izolacją), na przykład płytkami kondensatora lub przewodzącymi drutami kablowymi, wzrasta natężenie (natężenie) pola elektrycznego w dielektryku. Siła pola elektrycznego w dielektryku również wzrasta wraz ze zmniejszaniem się odległości między przewodami.

Przy określonym natężeniu pola następuje przebicie dielektryka, powstaje iskra lub łuk i w obwodzie pojawia się prąd elektryczny. Natężenie pola elektrycznego, przy którym następuje przebicie izolacji, nazywane jest wytrzymałością elektryczną izolacji Epr.

Wytrzymałość dielektryczna jest definiowana jako napięcie na mm grubości izolacji i jest mierzona w V/mm (kV/mm) lub kV/cm. Na przykład wytrzymałość dielektryczna powietrza między gładkimi płytami wynosi 32 kV / cm.

Natężenie pola elektrycznego w dielektryku w przypadku, gdy przewodniki mają postać płytek lub pasków oddzielonych równą szczeliną (na przykład w kondensatorze papierowym) oblicza się według wzoru

mi = U / d,

gdzie U jest napięciem między przewodami, V (kV); d — grubość warstwy dielektrycznej, mm (cm).

Przykłady

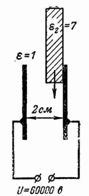
1. Jakie jest natężenie pola elektrycznego w szczelinie powietrznej o grubości 3 cm między płytami, jeśli napięcie między nimi wynosi U = 100 kV (rys. 1)?

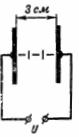
Ryż. 1.

Natężenie pola elektrycznego wynosi: E = U / d = 100000/3 = 33333 V / cm.

Takie napięcie przekracza wytrzymałość dielektryczną powietrza (32 kV/cm) i istnieje ryzyko zniszczenia.

Ryzyku uszkodzenia DC można zapobiec, zwiększając szczelinę np. do 5 cm lub stosując inną, mocniejszą izolację zamiast powietrza, np. karton elektryczny (rys. 2).

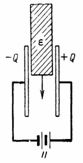
Ryż. 2.

Tektura elektryczna ma stałą dielektryczną ε = 2 i wytrzymałość dielektryczną 80 000 V/cm. W naszym przypadku natężenie pola elektrycznego w izolacji wynosi 33333 V. Powietrze nie może wytrzymać tej siły, podczas gdy karton elektryczny w tym przypadku ma rezerwę wytrzymałości dielektrycznej 80 000/33333 = 2,4, ponieważ wytrzymałość dielektryczna puszki elektrycznej wynosi 80 000/32 000 = 2,5 razy więcej niż powietrze.

2. Jakie jest natężenie pola elektrycznego w dielektryku kondensatora o grubości 3 mm, jeśli kondensator jest podłączony do napięcia U = 6 kV?

E = U / d = 6000 / 0,3 = 20000 V / cm.

3. Dielektryk o grubości 2 mm rozkłada się pod napięciem 30 kV. Jaka była jego siła elektryczna?

E = U / d = 30 000 / 0,2 = 150 000 V / cm = 150 kV / cm. Szkło ma taką siłę elektryczną.

4. Przestrzeń między okładkami kondensatora jest wypełniona warstwami tektury elektrycznej i warstwą miki o tej samej grubości (ryc. 3). Napięcie między okładkami kondensatora wynosi U = 10000 V. Karton elektryczny ma stałą dielektryczną ε1 = 2 i mikę ε2 = 8.Jak rozłoży się napięcie U pomiędzy warstwami izolacji i jakie będzie natężenie pola elektrycznego w poszczególnych warstwach?

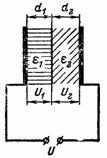
Ryż. 3.

Napięcia U1 i U2 na warstwach dielektryka o tej samej grubości nie będą sobie równe. Napięcie kondensatora zostanie podzielone na napięcia U1 i U2, które będą odwrotnie proporcjonalne do stałych dielektrycznych:

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2.

Ponieważ U = U1 + U2, mamy dwa równania z dwiema niewiadomymi.

Podstaw pierwsze równanie do drugiego: U = 4 ∙ U2 + U2 = 5 ∙ U2.

Dlatego 10000 V = 5 ∙ U2; U2 = 2000 V; U1 = 4, U2 = 8000 V.

Chociaż warstwy dielektryczne mają tę samą grubość, nie są jednakowo naładowane. Dielektryk o większej stałej dielektrycznej jest mniej obciążony (U2 = 2000 V) i odwrotnie (U1 = 8000 V).

Natężenie pola elektrycznego E w warstwach dielektryka jest równe:

E1 = U1 / d1 = 8000 / 0,2 = 40 000 V / cm;

E2 = U2 / d2 = 2000 / 0,2 = 10000 V / cm.

Różnica stałej dielektrycznej prowadzi do wzrostu natężenia pola elektrycznego. Gdyby całą szczelinę wypełnić tylko jednym dielektrykiem, na przykład miką lub tekturą elektryczną, natężenie pola elektrycznego byłoby mniejsze, ponieważ rozkładałoby się w szczelinie dość równomiernie:

mi = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0,4 = 25000 V / cm.

Dlatego konieczne jest unikanie stosowania złożonej izolacji o bardzo różnych stałych dielektrycznych. Z tego samego powodu ryzyko awarii wzrasta, gdy w izolacji tworzą się pęcherzyki powietrza.

5. Wyznacz natężenie pola elektrycznego w dielektryku kondensatora z poprzedniego przykładu, jeśli grubość warstw dielektryka nie jest taka sama.Płytka elektryczna ma grubość d1 = 0,2 mm i mikę d2 = 3,8 mm (rys. 4).

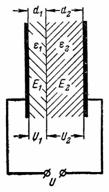
Ryż. 4.

Natężenie pola elektrycznego będzie rozkładać się odwrotnie proporcjonalnie do stałych dielektrycznych:

E1 / E2 = ε2 / ε1 = 8/2 = 4.

Skoro E1 = U1 / d1 = U1 / 0,2 i E2 = U2 / d2 = U2 / 3,8, to E1 / E2 = (U1 / 0,2) / (U2 / 3,8) = (U1 ∙ 3,8) / (0,2 ∙ U2) = 19 ∙ U1 / U2.

Dlatego E1 / E2 = 4 = 19 ∙ U1 / U2, czyli U1 / U2 = 4/19.

Suma napięć U1 i U2 na warstwach dielektrycznych jest równa napięciu źródła U: U = U1 + U2; 10000 = U1 + U2.

Skoro U1 = 4/19 ∙ U2, to 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2; U2 = 190 000 /23 = 8260 V; U1 = U-U2 = 1740 V.

Natężenie pola elektrycznego w mice wynosi E2 ∙ 8260 / 3,8≈2174 V / cm.

Mika ma wytrzymałość elektryczną 80 000 V / mm i może wytrzymać takie napięcie.

Natężenie pola elektrycznego w kartonie elektrycznym wynosi E1 = 1740 / 0,2 = 8700 V / mm.

Karton elektryczny nie wytrzyma takiego napięcia, ponieważ jego wytrzymałość dielektryczna wynosi tylko 8000 V / mm.

6. Do dwóch metalowych płytek oddalonych od siebie o 2 cm podłączono napięcie 60 000 V. Wyznacz natężenie pola elektrycznego w szczelinie powietrznej oraz natężenie pola elektrycznego w powietrzu i szkle, jeśli w szczelinie jest szkło. grubości 1 cm (ryc. 5).

Ryż. 5.

Jeśli między płytami znajduje się tylko powietrze, natężenie pola elektrycznego w nim jest równe: E = U / d = 60 000 /2 = 30 000 V / cm.

Natężenie pola jest zbliżone do wytrzymałości dielektrycznej powietrza.Jeśli do szczeliny wprowadzi się płytkę szklaną o grubości 1 cm (stała dielektryczna szkła ε2 = 7), to E1 = U1 / d1 = U1 / 1 = U1; E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60 000-U2; 8 ∙ U2 = 60 000; U2 = 7500 V; E2 = U2 / d2 = 7500 V / cm.

Natężenie pola elektrycznego w szkle wynosi E2 = 7,5 kV/cm, a jego natężenie elektryczne to 150 kV/cm.

W tym przypadku szkło ma 20-krotny współczynnik bezpieczeństwa.

Dla szczeliny powietrznej mamy: U1 = 60 000-7500 = 52500 V; E1 = U1 / d1 = 52500 V / cm.

W tym przypadku siła pola elektrycznego w szczelinie powietrznej jest większa niż w pierwszej, bez szkła. Po włożeniu szkła cała kombinacja ma mniejszą wytrzymałość niż samo powietrze.

Ryzyko stłuczenia występuje również wtedy, gdy grubość tafli szklanej jest równa szczelinie między płytkami przewodzącymi, tj. 2 cm, ponieważ w szczelinie, która zostanie przebita, nieuchronnie pozostaną cienkie szczeliny powietrzne.

Wytrzymałość dielektryczna szczeliny między przewodami wysokiego napięcia musi być wzmocniona materiałami o niskiej stałej dielektrycznej i wysokiej wytrzymałości dielektrycznej, na przykład tekturą elektryczną o ε = 2. Unikaj kombinacji materiałów o wysokiej stałej dielektrycznej (szkło , porcelana) i powietrza, które należy zastąpić olejem.