Obliczenia obwodów magnetycznych

W maszynach i urządzeniach elektrycznych strumień magnetyczny F koncentruje się w obwodzie magnetycznym (rdzeń ferromagnetyczny) i szczelinach powietrznych tego obwodu magnetycznego. Ta ścieżka strumienia magnetycznego nazywana jest obwodem magnetycznym.

Obwód magnetyczny jest jak obwód elektryczny. Strumień magnetyczny Ф przypomina prąd elektryczny I, indukcja В przypomina gęstość prądu, siła magnesująca (ns) Fн (H ∙ l = I ∙ ω) odpowiada e. itp. z

W najprostszym przypadku obwód magnetyczny ma wszędzie taki sam przekrój i jest wykonany z jednorodnego materiału magnetycznego. Aby określić n. gdzie l ∙ ω wymagane do zapewnienia wymaganej indukcji B, odpowiednie natężenie H jest wyznaczane z krzywej namagnesowania i mnożone przez średnią długość linii pola magnetycznego l: H ∙ l = I ∙ ω = Fm.

Stąd określa się wymagany prąd I lub liczbę zwojów ω cewki.

Złożony obwód magnetyczny zwykle ma sekcje z różnymi sekcjami i materiałami magnetycznymi. Sekcje te są zwykle połączone szeregowo, dlatego przez każdą z nich przechodzi ten sam strumień magnetyczny F.Indukcja B w każdym przekroju zależy od przekroju przekroju i jest obliczana dla każdego przekroju osobno ze wzoru B = Φ∶S.

Dla różnych wartości indukcji intensywność H jest określana na podstawie krzywej namagnesowania i mnożona przez średnią długość linii elektroenergetycznej odpowiedniego odcinka obwodu. Podsumowując poszczególne prace, otrzymuje się pełne n. c. obwód magnetyczny:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … co określa prąd magnesujący lub liczbę zwojów cewki.

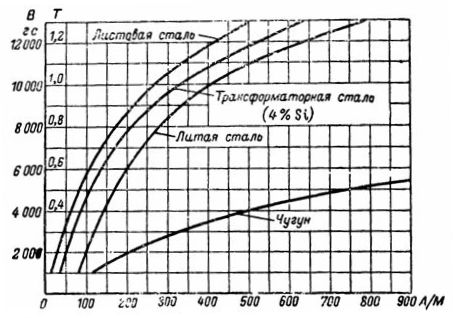
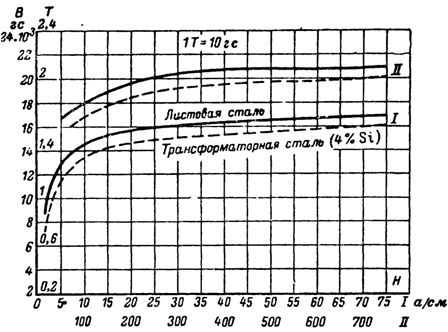
Krzywe namagnesowania

Przykłady

1. Jaki musi być prąd magnesujący I cewki o 200 zwojach, aby n. c. wytworzył w żeliwnym pierścieniu strumień magnetyczny Ф = 15700 Ms = 0,000157 Wb? Średni promień pierścienia żeliwnego wynosi r = 5 cm, a średnica jego przekroju d = 2 cm (rys. 1).

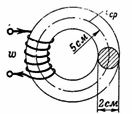
Ryż. 1.

Przekrój obwodu magnetycznego S = (π ∙ d ^ 2) / 4 = 3,14 cm2.

Indukcja w rdzeniu wynosi: B = Φ∶S = 15700∶3,14 = 5000 G.

W systemie MKSA indukcja wynosi: B = 0,000157 Wb: 0,0000314 m2 = 0,5 T.

Z krzywej magnesowania żeliwa znajdujemy wymaganą siłę H równą 750 A / m dla B = 5000 G = 0,5 T. Siła magnesowania jest równa: I ∙ ω = H ∙ l = 235,5 Av.

Dlatego wymagany prąd I = (H ∙ l) / ω = 235,5 / 200 = 1,17 A.

2. Zamknięty obwód magnetyczny (rys. 2) wykonany jest ze stalowych płyt transformatora. Ile zwojów musi się znajdować w cewce, w której płynie prąd o natężeniu 0,5 A, aby w rdzeniu wytworzył się strumień magnetyczny Ф = 160000 Ms = 0,0016 Wb?

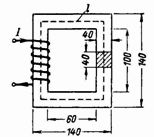
Ryż. 2.

Przekrój rdzenia S = 4 ∙ 4 = 16 cm2 = 0,0016 m2.

Indukcja rdzenia B = F / S = 160000/16 = 10000 Gs = 1 T.

Zgodnie z krzywą namagnesowania stali transformatorowej, dla B = 10 000 Gs = 1 T natężenie H = 3,25 A/cm = 325 A/m.

Średnia długość linii pola magnetycznego wynosi l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0,48 m.

Siła magnesująca Fm = I ∙ ω = H ∙ l = 3,25 ∙ 48 = 315 ∙ 0,48 = 156 Śr.

Przy prądzie 0,5 A liczba zwojów wynosi ω = 156 / 0,5 = 312.

3. Obwód magnetyczny pokazany na ryc. 3 jest podobny do obwodu magnetycznego z poprzedniego przykładu, z wyjątkiem tego, że ma szczelinę powietrzną δ = 5 mm. Jaki powinien być n. s. i prąd cewki tak, aby strumień magnetyczny był taki sam jak w poprzednim przykładzie, czyli F = 160000 Ms = 0,0016 Wb?

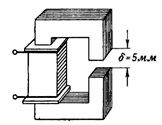
Ryż. 3.

Obwód magnetyczny ma dwa połączone szeregowo odcinki, których przekrój jest taki sam jak w poprzednim przykładzie, czyli S = 16 cm2. Indukcyjność jest również równa B = 10000 G = 1 T.

Średnia długość stalowej linii magnetycznej jest nieco krótsza: lс = 48-0,5 = 47,5 cm ≈0,48 m.

Napięcie magnetyczne w tej sekcji obwodu magnetycznego wynosi Hc ∙ lc = 3,25 ∙ 48≈156 Av.

Natężenie pola w szczelinie powietrznej wynosi: Hδ = 0,8 ∙ B = 0,8 ∙ 10000 = 8000 A / cm.

Naprężenie magnetyczne w przekroju poprzecznym szczeliny powietrznej Hδ ∙ δ = 8000 ∙ 0,5 = 4000 Śr.

Ukończ n. c. jest równe sumie napięć magnetycznych w poszczególnych sekcjach: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. ja = (ja ∙ ω) / ω = 4156/312 = 13,3 A.

Jeśli w poprzednim przykładzie wymagany strumień magnetyczny był dostarczany przez prąd 0,5 A, to dla obwodu magnetycznego ze szczeliną powietrzną 0,5 cm potrzebny jest prąd 13 A, aby uzyskać ten sam strumień magnetyczny. Z tego widać, że szczelina powietrzna, nawet niewielka w stosunku do długości obwodu magnetycznego, znacznie zwiększa wymagane n. v. i prąd cewki.

4. Obliczono, że strumień magnetyczny transformatora wynosi F = 72000 Ms. Wymagane jest obliczenie n.si prąd magnesujący uzwojenia pierwotnego mający 800 zwojów. W rdzeniu transformatora znajduje się przerwa δ = 0,2 mm. Wymiary rdzenia transformatora pokazano na ryc. 4. Przekrój rdzenia S = 2 ∙ 3 ​​​​​​= 6 cm2 (transformatory z rdzeniami o takim kształcie nazywane są pancernymi).

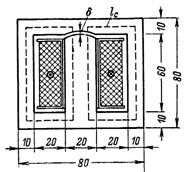
Ryż. 4.

Indukcja rdzenia i szczeliny powietrznej B = F / S = 72000/6 = 12000 G.

Na podstawie krzywej namagnesowania stali transformatorowej dla B = 12000 G określamy natężenie: Hc = 5 A/cm.

Średnia długość linii magnetycznej w stali wynosi lс = 2 ∙ (6 + 3) = 18 cm.

Napięcie w szczelinie powietrznej Hδ = 0,8 ∙ B = 9600 A / cm.

Siła magnesująca I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0,02 = 90 + 192 = 282 Av; ja = (ja ∙ ω) / ω = 282/800 = 0,35 A.

W rdzeniu pancernym strumień magnetyczny dzieli się na dwie części, które są zamknięte wzdłuż bocznych prętów, których przekrój wynosi S / 2, a średnia długość linii magnetycznej wynosi lc. W rezultacie obwód magnetyczny jest całkowicie analogiczny do obwodu magnetycznego konwencjonalnego transformatora ze wspólnym rdzeniem S i długością linii elektroenergetycznej lc.

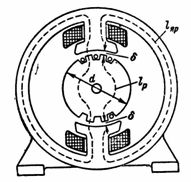
5. Strumień magnetyczny maszyny prądu stałego F = 1280000 Mks. Obwód magnetyczny zawiera stalowy jarzmo o średniej długości linii magnetycznej lа = 80 cm, wirnik złożony z płyt ze stali elektrycznej o średniej długości pola lp = 18 cm oraz dwie szczeliny powietrzne δ 0,2 cm każda. = 8 ∙ 20 cm2; przekrój wirnika i bieguna Sр = 12 ∙ 20 cm2... Oblicz n. p. i liczba zwojów cewki biegunowej, jeżeli maksymalny prąd magnesujący (wzbudzający) w niej wynosi 1 A (ryc. 5).

Ryż. 5.

Indukcja w jarzmie i na biegunie Bя = Ф / Sя = 1280000/160 = 8000 G.

Napięcie w jarzmie i biegunie zgodnie z krzywą magnesowania staliwa przy Bя = 8000 G jest równe:

H = 2,8 A / cm.

Siła magnesowania w przekroju jarzma HЯ ∙ la = 2,8 ∙ 80 = 224 Av.

Indukcja w wirniku, biegunie i szczelinie powietrznej Br = Ф / Ср = 1280000/240 = 5333 G.

Napięcie w wirniku wykonanym z blach stalowych przy Br=5333 Gs Hrp=0,9 A/cm,

a napięcie magnetyczne sekcji wirnika Hр ∙ lр = 0,9 ∙ 18 = 16,2 Av.

Napięcie w szczelinie powietrznej Hδ = 0,8 ∙ Bδ = 0,8 ∙ 5333 = 4266,4 A / cm.

Napięcie magnetyczne w przekroju szczeliny powietrznej Hδ ∙ 2 ∙ δ = 4266,4 ∙ 2 ∙ 0,2 = 1706,56 A.

Ukończ n. c. równe sumie napięć magnetycznych w poszczególnych sekcjach: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; ja ∙ ω = 224 + 16,2 + 1706,56 = 1946,76 śr.

Liczba zwojów w cewkach dwubiegunowych ω = (I ∙ ω) / I = 1946,76 / 1≈2000.