Siła pociągowa elektromagnesów
Siła, z jaką elektromagnes przyciąga materiały ferromagnetyczne, zależy od strumienia magnetycznego F lub równoważnie od indukcji B i pola przekroju poprzecznego elektromagnesu S.
Siła nacisku elektromagnesu jest określona wzorem
F = 40550 ∙ B ^ 2 ∙ S,
gdzie F jest siłą nacisku elektromagnesu, kg (siła jest również mierzona w niutonach, 1 kg = 9,81 N lub 1 N = 0,102 kg); B — indukcja, T; S to pole przekroju poprzecznego elektromagnesu, m2.
Przykłady
1. Elektromagnes kranu jest obwodem magnetycznym (ryc. 1). Jaka jest siła podnoszenia elektromagnesu podkowy, jeśli indukcja magnetyczna wynosi B = 1 T, a pole przekroju poprzecznego każdego bieguna elektromagnesu wynosi S = 0,02 m2 (ryc. 1, b)? Pomiń wpływ szczeliny między elektromagnesem a twornikiem.
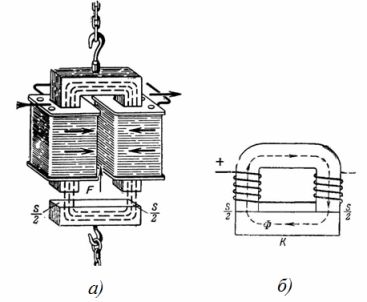
Ryż. 1. Elektromagnes podnoszący
F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.
2. Okrągły stalowy elektromagnes ma wymiary pokazane na ryc. 2, aib. Siła podnoszenia elektromagnesu wynosi 3 T. Określ pole przekroju poprzecznego rdzenia elektromagnesu, n. p. i liczba zwojów cewki przy prądzie magnesującym I = 0,5 A.
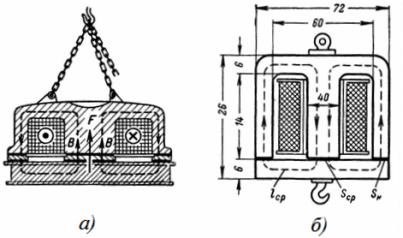
Ryż. 2. Okrągły elektromagnes
Strumień magnetyczny przechodzi przez okrągły wewnętrzny rdzeń i powraca przez cylindryczny korpus. Pola przekroju poprzecznego rdzenia Sc i obudowy Sk są w przybliżeniu takie same, dlatego wartości indukcji w rdzeniu i obudowie są praktycznie takie same:
Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,
Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;
S = Sc + Sk = 0,24995 m2 ≈0,25 m2.
Wymaganą indukcję w elektromagnesie określa wzór F = 40550 ∙ B ^ 2 ∙ S,
gdzie B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.
Napięcie przy tej indukcji znajduje się na krzywej namagnesowania staliwa:
H = 180 A / m.
Średnia długość linii pola (ryc. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.
Siła magnesująca I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; ja = (ja ∙ ω) / ja = 154,8 / 0,5 = 310 A.
Właściwie n. s, to znaczy prąd i liczba zwojów, muszą być wielokrotnie większe, ponieważ między elektromagnesem a twornikiem występuje nieunikniona szczelina powietrzna, co znacznie zwiększa opór magnetyczny obwodu magnetycznego. Dlatego przy obliczaniu elektromagnesów należy wziąć pod uwagę szczelinę powietrzną.
3. Cewka elektromagnesu do kranu ma 1350 zwojów, przepływa przez nią prąd I = 12 A. Wymiary elektromagnesu pokazano na ryc. 3. Jaki ciężar podnosi elektromagnes w odległości 1 cm od zwory i jaki ciężar może utrzymać po grawitacji?
Ryż. 3. Cewka elektromagnetyczna
Większość N. o I ∙ ω zużywana jest na przewodzenie strumienia magnetycznego przez szczelinę powietrzną: I ∙ ω≈Hδ ∙ 2 ∙ δ.
Siła magnesująca I ∙ ω = 12 ∙ 1350 = 16200 A.
Skoro H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, to Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.
Zatem 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, tj. B = 1,012T.
Zakładamy, że indukcja wynosi B = 1 T, ponieważ część n. c. I ∙ ω zużywa się na przewodzenie strumienia magnetycznego w stali.
Sprawdźmy to obliczenie za pomocą wzoru I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.
Średnia długość linii magnetycznej wynosi: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.
Intensywność Hc przy B = 1 T (10000 Gs) wyznacza się z krzywej namagnesowania:
Hc = 260 A / m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Śr.
Siła magnesująca I ∙ ω = 16114 Av tworząca indukcję B = 1 T jest praktycznie równa podanemu n. v. I ∙ ω = 16200 Śr.
Całkowite pole przekroju rdzenia i stożka wynosi: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.
Elektromagnes przyciągnie ładunek o masie F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg z odległości 1 cm.
Ponieważ szczelina powietrzna praktycznie znika po przyciągnięciu twornika, elektromagnes może wytrzymać znacznie większe obciążenie. W tym przypadku cały n. c. I ∙ ω zużywa się na przewodzenie strumienia magnetycznego tylko w stali, dlatego I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.
Przy takim napięciu stal jest praktycznie nasycona, a indukcja w niej wynosi około 2 T. Elektromagnes przyciąga twornik z siłą F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.
4. Przekaźnik sygnałowy (migający) składa się z opancerzonego elektromagnesu 1 z okrągłym rdzeniem i zwory 2 typu zaworowego, który po dostarczeniu prądu do elektromagnesu przyciąga i zwalnia migacz 3, który otwiera cyfrę sygnału (ryc. 4).
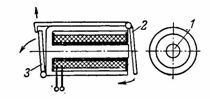
Ryż. 4. Elektromagnes pancerza
Siła magnesowania wynosi I ∙ ω = 120 Av, szczelina powietrzna wynosi δ = 0,1 cm, a całkowita powierzchnia przekroju elektromagnesu wynosi S = 2 cm2. Oszacuj siłę przyciągania przekaźnika.
Indukcyjność B wyznacza się przez kolejne przybliżenia za pomocą równania I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.
Niech n. c. Hc ∙ lc wynosi 15% I ∙ ω, tj. 18 Av.
Wtedy ja ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102 / 0,2 = 510 A / cm = 51000 A / m.
Stąd znajdujemy indukcję B:
Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0,0637 T.
Po podstawieniu wartości B we wzorze F = 40550 ∙ B ^ 2 ∙ S otrzymujemy:
F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.
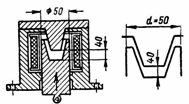
5. Cewka hamulca prądu stałego (rys. 5) ma zworę tłoka ze stożkowym ogranicznikiem. Odległość między twornikiem a rdzeniem wynosi 4 cm, a średnica robocza (rdzenie o okrągłym polu styku) d = 50 mm. Twornik jest wciągany do cewki z siłą 50 kg. Długość środkowej linii siły lav = 40 cm Wyznacz n. s. i prąd cewki, jeśli jest 3000 zwojów.
Ryż. 5. Cewka hamulca prądu stałego
Powierzchnia sekcji roboczej elektromagnesu jest równa powierzchni koła o średnicy d = 5 cm:
S = (π ∙ re ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.
Indukcję B potrzebną do wytworzenia siły F = 50 kg obliczamy z równania F = 40550 ∙ B ^ 2 ∙ S,
gdzie B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.
Siła magnesująca I ∙ ω = Hс ∙ lс + Hδ ∙ δ.
Siłę magnesowania dla stali Hc ∙ lc wyznaczamy w sposób uproszczony, opierając się na fakcie, że wynosi ona 15% I ∙ ω:
ja ∙ ω = 0,15 ∙ ja ∙ ω + Hδ ∙ δ; 0,85 ∙ ja ∙ ω = Hδ ∙ δ; 0,85 ∙ ja ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; ja ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30 000 Śr.
Prąd magnesujący I = (I ∙ ω) / ω = 30000/3000 = 10 A.