Obliczanie pojemności kondensatora

Pojemność C to zdolność kondensatora do przyjmowania (przechowywania i utrzymywania) ilości energii elektrycznej Q w amperosekundach lub ładunku Q w wisiorkach. Jeżeli ciału, np. piłce, powiemy ładunek elektryczny (ilość elektryczności) Q, to elektroskop podłączony między tym ciałem a ziemią wskaże napięcie U (rys. 1). Napięcie to jest proporcjonalne do ładunku, a także zależy od kształtu i wielkości ciała.

Zależność między ładunkiem Q a napięciem U wyraża wzór Q = C ∙ U.

Stała proporcjonalności C nazywana jest pojemnością ciała. Jeżeli ciało ma kształt kuli, to pojemność ciała jest proporcjonalna do promienia kuli r.

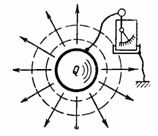
Ryż. 1.

Jednostką miary pojemności jest farad (F).

Ciało ma pojemność 1 F, gdy ładunek 1 k wytwarza między nim a ziemią napięcie 1 V. Farady to bardzo duża jednostka miary, dlatego w praktyce stosuje się mniejsze jednostki: mikrofarad (μF), nanofarad (nF) i pikofarad (pF)...

Jednostki te są powiązane następującymi stosunkami: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Pojemność kuli o promieniu 1 cm wynosi 1,1 pF.

Nie tylko izolowane ciało może gromadzić ładunek, ale także specjalne urządzenie zwane kondensatorem. Kondensator składa się z dwóch lub więcej płytek (płyt), które są oddzielone dielektrykiem (izolacją).

na ryc. 2 przedstawia obwód ze źródłem prądu stałego podłączonym do kondensatora. Po włączeniu na prawej okładce kondensatora tworzy się ładunek dodatni +Q, a na lewej ładunek ujemny –Q. Podczas ładunek kondensatora prąd przepływa przez obwód, który zatrzymuje się po zakończeniu ładowania; wtedy napięcie na kondensatorze będzie równe e. itp. c. źródło U. Ładunek na okładce kondensatora, napięcie i pojemność są powiązane stosunkiem Q = C ∙ U. W tym przypadku w dielektryku kondensatora powstaje pole elektrostatyczne.

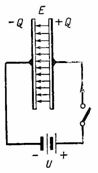
Ryż. 2.

Pojemność kondensatora z dielektrykiem powietrza można obliczyć za pomocą wzoru C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, gdzie S jest powierzchnią jednej płytki, cm2; d to odległość między płytami, cm; C to pojemność kondensatora, pF.

Pojemność kondensatora złożonego z n okładek (rys. 3) jest równa: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

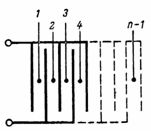
Ryż. 3.

Jeśli przestrzeń między okładkami wypełnimy innym dielektrykiem, na przykład papierem, pojemność kondensatora wzrośnie o współczynnik ε. W przypadku zastosowania izolacji papierowej pojemność wzrośnie 3-krotnie, w przypadku izolacji mikowej — 5-8 razy, w przypadku szkła — 7-krotnie itd. Wartość ε nazywana jest stałą dielektryczną dielektryka.

Ogólny wzór na określenie pojemności kondensatora o stałej dielektrycznej ε (epsilon) to: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Ta formuła jest przydatna do obliczania małych kondensatorów zmiennych do radia.Ten sam wzór można przedstawić jako: C = (ε_0 ∙ ε ∙ S) / d, gdzie ε_0 jest stałą dielektryczną lub stałą dielektryczną próżni (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε jest stałą dielektryczną dielektryka.

W tym wzorze wymiary są zastępowane w metrach, a pojemność jest uzyskiwana w faradach.

Przykłady

1. Jaka jest pojemność planety Ziemia, której promień wynosi r = 6378 km?

Ponieważ pojemność kuli o promieniu 1 cm jest równa 1,11 pF, pojemność Ziemi wynosi: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Pojemność kuli wielkości naszej planety jest stosunkowo niewielka. Taką pojemność mają małe kondensatory elektrolityczne).

2. Wyznacz pojemność kondensatora składającego się z dwóch okładek, z których każda ma powierzchnię S = 120 cm2.

Płyty są oddzielone warstwą powietrza o grubości d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF .. .

3. Wyznacz pojemność kondensatora na podstawie danych podanych w poprzednim przykładzie, jeśli przestrzeń między okładkami jest wypełniona papierem woskowym o stałej dielektrycznej ε = 4, szkłem (ε = 7), tekturą elektryczną (ε = 2) , mika (ε = 8).

Kondensator z woskowanego papieru ma pojemność C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Pojemność kondensatora szklanego wynosi C = 7 ∙ 21,2 = 148,4 pF.

Pojemność kartonowego kondensatora wynosi C = 2 ∙ 21,2 = 42,3 pF.

Pojemność kondensatora mikowego wynosi C = 8 ∙ 21,2 = 169,6 pF.

4. Jaka jest pojemność powietrznego kondensatora obrotowego dla odbiornika radiowego składającego się z 20 płytek o powierzchni 20 cm2, jeśli odległość między płytkami wynosi 0,06 cm (ryc. 149)?

do = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ re) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Kondensator pokazany na rys.3, składa się z oddzielnych najprostszych kondensatorów z dwoma okładkami, których liczba jest równa n-1.

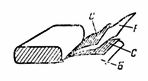
5. Kondensator papierowy o pojemności C = 2 μF składa się z dwóch pasków folii aluminiowej C i dwóch pasków dielektryka wykonanego z woskowanego papieru B o stałej dielektrycznej ε = 6. Grubość woskowanego papieru wynosi d = 0,1 mm. Zagięte paski są zwijane, wyprowadzenia wykonane są z blach stalowych. Wyznacz długość taśmy stalowej skraplacza, jeżeli jej szerokość wynosi 4 cm (rys. 4).

Ryż. 4.

Najpierw określamy powierzchnię jednego paska za pomocą wzoru C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, skąd S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Długość każdego pasa wynosi l = 37680/4 = 9420 cm = 94,2 m.