Siła pola magnetycznego. Siła magnesująca

Przez drut lub cewkę zawsze przepływa prąd elektryczny pole magnetyczne… Pole magnetyczne magnesu trwałego jest spowodowane ruchem elektronów po ich orbitach w atomie.

Pole magnetyczne charakteryzuje się swoją siłą. Siła H pola magnetycznego jest podobna do wytrzymałości mechanicznej. Jest to wielkość wektorowa, to znaczy ma wielkość i kierunek.

Pole magnetyczne, czyli przestrzeń wokół magnesu, można przedstawić jako wypełnione liniami magnetycznymi, które, jak się uważa, wychodzą z bieguna północnego magnesu i wchodzą do bieguna południowego (ryc. 1). Styczne do linii magnetycznej wskazują kierunek natężenia pola magnetycznego.

Pole magnetyczne jest silniejsze tam, gdzie linie magnetyczne są gęstsze (na biegunach magnesu lub wewnątrz cewki przewodzącej prąd).

Im większy prąd I i liczba zwojów ω cewki, tym większe pole magnetyczne w pobliżu drutu (lub wewnątrz cewki).

Siła pola magnetycznego H w dowolnym punkcie przestrzeni jest tym większa, im większy jest iloczyn ∙ ω i im krótsza jest długość linii magnetycznej:

H = (ja ∙ ω) / l.

Z równania wynika, że ​​​​jednostką pomiaru natężenia pola magnetycznego jest amper na metr (A / m).

Dla każdej linii magnetycznej w danym jednorodnym polu iloczyny H1 ∙ l1 = H2 ∙ l2 = … = H ∙ l = I ∙ ω są sobie równe (rys. 1).

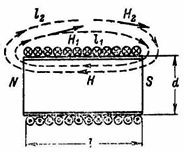
Ryż. 1.

Iloczyn H ∙ l w obwodach magnetycznych jest podobny do napięcia w obwodach elektrycznych i nazywany jest napięciem magnetycznym, a mierzony wzdłuż całej długości linii indukcji magnetycznej nazywany jest siłą magnesującą (ns) Fm: Fm = H ∙ l = ja ∙ ω.

Siłę magnesującą Fm mierzy się w amperach, ale w praktyce technicznej zamiast nazwy amper używa się nazwy amperokręt, która podkreśla, że ​​Fm jest proporcjonalne do prądu i liczby zwojów.

Dla cylindrycznej cewki bez rdzenia, której długość jest znacznie większa niż jej średnica (l≫d), pole magnetyczne wewnątrz cewki można uznać za jednorodne, tj. przy takim samym natężeniu pola magnetycznego H w całej przestrzeni wewnętrznej cewki (rys. 1). Ponieważ pole magnetyczne na zewnątrz takiej cewki jest znacznie słabsze niż wewnątrz niej, zewnętrzne pole magnetyczne można pominąć iw obliczeniach przyjąć, że n. cewka c jest równa iloczynowi natężenia pola wewnątrz cewki i długości cewki.

Biegunowość pola magnetycznego drutu i cewki prądowej jest określona przez regułę gimbala. Jeśli ruch gimbala do przodu pokrywa się z kierunkiem prądu, to kierunek obrotu uchwytu gimbala będzie wskazywał kierunek linii magnetycznych.

Przykłady

1. Prąd o natężeniu 3 A przepływa przez cewkę zawierającą 2000 zwojów. co to jest n. v. cewki?

Fm = I ∙ ω = 3 ∙ 2000 = 6000 A. Siła magnesowania cewki wynosi 6000 amperozwojów.

2. Cewka z 2500 zwojami powinna mieć n. str. 10000 A. Jaki prąd musi przez nią płynąć?

ja = Fm / ω = (I ∙ ω) / ω = 10000/2500 = 4 A.

3.Przez cewkę przepływa prąd I = 2 A. Ile zwojów musi być w cewce, aby zapewnić n. wieś 8000 A?

ω = Fm / I = (I ∙ ω) / I = 8000/2 = 4000 obrotów.

4. Wewnątrz cewki o długości 10 cm ze 100 zwojami należy zapewnić natężenie pola magnetycznego H = 4000 A / m. Jaki prąd powinna przewodzić cewka?

Siła magnesująca cewki wynosi Fm = H ∙ l = I ∙ ω. Dlatego 4000 A / m ∙ 0,1 m = I ∙ 100; ja = 400/100 = 4 A.

5. Średnica cewki (solemagnesu) wynosi D = 20 mm, a jej długość wynosi l = 10 cm Cewka jest nawinięta z drutu miedzianego o średnicy d = 0,4 mm. Jakie jest natężenie pola magnetycznego wewnątrz cewki, jeśli jest ona włączona przy napięciu 4,5 V?

Liczba zwojów bez uwzględnienia grubości izolacji ω = l∶d = 100∶0,4 = 250 zwojów.

Długość pętli π ∙ d = 3,14 ∙ 0,02 m = 0,0628 m.

Długość zwoju l1 = 250 ∙ 0,0628 m = 15,7 m.

Rezystancja czynna cewki r = ρ ∙ l1 / S = 0,0175 ∙ (4 ∙ 15,7) / (3,14 ∙ 0,16) = 2,2 Ohm.

Prąd I = U / r = 4,5 / 2,2 = 2,045 A ≈2 A.

Siła pola magnetycznego wewnątrz cewki H = (I ∙ ω) / l = (2 ∙ 250) / 0,1 = 5000 A / m.

6. Wyznacz natężenie pola magnetycznego w odległości 1, 2, 5 cm od prostego przewodu, przez który płynie prąd I = 100 A.

Użyjmy wzoru H ∙ l = I ∙ ω.

Dla drutu prostego ω = 1 i l = 2 ∙ π ∙ r,

skąd H = I / (2 ∙ π ∙ r).

H1 = 100 / (2 ∙ 3,14 ∙ 0,01) = 1590 A / m; H2 = 795 A/m; H3 = 318 A/m.