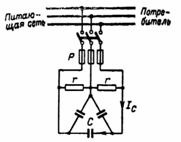
Obliczenia poprawy współczynnika mocy w sieci trójfazowej
Obliczając pojemność kondensatora w celu poprawy współczynnika mocy w sieci trójfazowej, będziemy przestrzegać tej samej kolejności, co w artykule z przykładami obliczeń w sieci jednofazowej… Wartość współczynnika mocy określa wzór mocy dla prądu trójfazowego:
P1 = √3 ∙ U ∙ ja ∙ cosφ, cosφ = P1 / (√3 ∙ U ∙ ja).
Przykłady
1. Trójfazowy silnik indukcyjny ma następujące dane panelowe: P = 40 kW, U = 380 V, I = 105 A, η = 0,85, f = 50 Hz. Połączenie gwiazdowe stojana. Załóżmy, że trudno jest określić wartość cosφ planszy, a zatem konieczne jest jej wyznaczenie. Do jakiej wartości zmniejszy się prąd po poprawie współczynnika mocy do cosφ = 1 za pomocą kondensatorów? Jaką pojemność powinny mieć kondensatory? Jaką moc bierną kompensują kondensatory (rys. 1)?
Zaciski uzwojenia stojana są oznaczone: początek — C1, C2, C3, końce — odpowiednio C4, C5, C6.W dalszej części jednak dla ułatwienia komunikacji ze schematami początek będzie oznaczony jako A, B, C, a końce X, Y, Z.
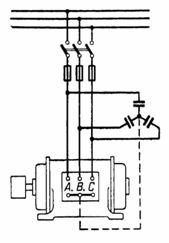
Ryż. 1.
Moc silnika P1 = P2 / η = 40000 / 0,85 ≈47000 W,
gdzie P2 to moc netto podana na tabliczce znamionowej silnika.
cosφ = P1 / (√3 ∙ U ∙ I) = 47000 / (√3 ∙ 380 ∙ 105) = 0,69.
Po poprawieniu współczynnika mocy do cosφ = 1 moc wejściowa wyniesie:
P1 = √3 ∙ U ∙ Ja ∙ 1
a prąd spadnie do
I1 = P1 / (√3 ∙ U) = 47000 / (1,73 ∙ 380) = 71,5 A.
Jest to prąd czynny przy cosφ = 0,69 od
Ia = I ∙ cosφ = 105 ∙ 0,69 = 71,5 A.
na ryc. 1 pokazuje włączenie kondensatorów w celu poprawy cosφ.
Napięcie kondensatora Uph = U / √3 = 380 / √3 = 220 V.
Fazowy prąd magnesujący jest równy liniowemu prądowi magnesującemu: IL = I ∙ sinφ = 105 ∙ 0,75 = 79,8 A.
Rezystancja pojemnościowa kondensatora, który musi dostarczać prąd magnesujący, wyniesie: xC = Uph / IL = 1 / (2 ∙ π ∙ f ∙ C).
Dlatego pojemność kondensatora C = IC / (Uph ∙ 2 ∙ π ∙ f) = 79,8 / (220 ∙ 3,14 ∙ 100) = 79,800 / (22 ∙ 3,14) ∙ 10 ^ (- 6) = 1156,4 μF.
Blok kondensatorów o łącznej pojemności C = 3 ∙ 1156,4≈3469 μF należy podłączyć do silnika trójfazowego, aby poprawić współczynnik mocy do cosφ = 1 i jednocześnie zmniejszyć prąd ze 105 do 71,5 A.
Całkowita moc bierna kompensowana przez kondensatory, która przy braku kondensatorów jest pobierana z sieci, Q = 3 ∙ Upph ∙ IL = 3 ∙ 220 ∙ 79,8≈52668 = 52,66 kvar.
W tym przypadku silnik pobiera moc czynną P1 = 47 kW tylko z sieci.
na ryc.2 przedstawia blok kondensatorów połączony w trójkąt i podłączony do zacisków silnika trójfazowego, którego uzwojenie jest również połączone w trójkąt. Takie połączenie kondensatorów jest korzystniejsze niż połączenie pokazane na ryc. 1 (patrz zakończenie obliczenia 2).
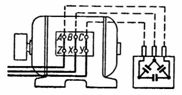
Ryż. 2.
2. Mała elektrownia zasila sieć trójfazową prądem I = 250 A przy napięciu sieci U = 380 V i współczynniku mocy sieci cosφ = 0,8. Poprawę współczynnika mocy zapewniają kondensatory połączone w trójkąt zgodnie ze schematem na rys. 3. Konieczne jest wyznaczenie wartości pojemności kondensatorów oraz skompensowanej mocy biernej.
Ryż. 3.
Moc pozorna S = √3 ∙ U ∙ I = 1,73 ∙ 380 ∙ 250 = 164,3 kVA.
Wyznacz moc czynną przy cosφ = 0,8:
P1 = √3 ∙ U ∙ I ∙ cosφ = S ∙ cosφ≈164,3 ∙ 0,8 = 131,5 W.
Moc bierna do kompensacji przy cosφ = 0,8
Q = S ∙ sinφ≈164,3 ∙ 0,6 = 98,6 kvar.
Dlatego liniowy prąd magnesujący (ryc. 3) IL = I ∙ sinφ = Q / (√3 ∙ U) ≈150 A.
Magnesujący (pojemnościowy) prąd fazowy ICph = Q / (3 ∙ U) = 98580 / (3 ∙ 380) = 86,5 A.
Prąd kondensatora można określić w inny sposób na podstawie prądu magnesującego (reaktywnego) w obwodzie:
IL = I ∙ sinφ = 250 ∙ 0,6 = 150 A,
ICph = ILph = IL / √3 = 150 / 1,73 = 86,7 A.
Każda grupa kondensatorów połączona w trójkąt ma napięcie 380 V i prąd fazowy ICph = 86,7 A.
ja = ICf = U / xC = U / (1⁄ (ω ∙ do)) = U ∙ ω ∙ do.
Dlatego C = IC / (U ∙ 2 ∙ π ∙ f) = 86,7 / (300 ∙ π ∙ 100) = 726 μF.
Całkowita pojemność baterii kondensatorów wynosi C3 = 3 ∙ 726 = 2178 μF.
Podłączone kondensatory umożliwiają wykorzystanie całej mocy elektrowni S = 164,3 kVA w postaci mocy netto.Bez kondensatorów roboczych wykorzystywana jest tylko moc czynna 131,5 kW przy cosφ = 0,8.
Skompensowana moc bierna Q = 3 ∙ U ∙ IC = 3 ∙ ω ∙ C ∙ U ^ 2 rośnie proporcjonalnie do kwadratu napięcia. Dlatego wymagana pojemność kondensatorów, a tym samym koszt kondensatorów, jest niższa, ponieważ napięcie jest wyższe.
Rezystancje r na ryc. 3 służą do stopniowego rozładowywania kondensatorów po ich odłączeniu od sieci.